《2025年初中必刷题七年级数学下册苏科版》

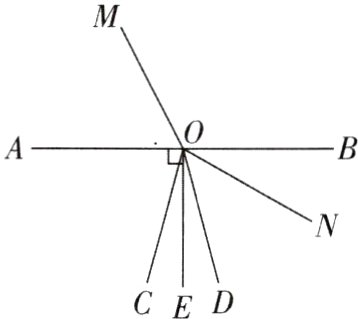
17（8分）[2024浙江金华质检]如图，$OE\perp AB$于点O，$\angle COE = 15^{\circ}$，射线OM从OA出发，绕点O以每秒$60^{\circ}$的速度顺时针向终边OB旋转，当OM到达OB时停止旋转.
（1）$\angle AOC$的度数为________.
（2）当OM旋转多少秒时，$\angle MOC = 105^{\circ}$？

答案： 17. 【解】
(1)因为$OE\perp AB$，所以$\angle AOE = 90^{\circ}$. 因为$\angle COE = 15^{\circ}$，所以$\angle AOC = 90^{\circ}-15^{\circ}=75^{\circ}$. 故答案为$75^{\circ}$.
(2)设旋转时间为$t$秒.
根据题意可得$\angle AOM=(60t)^{\circ}$.
当$0\lt t\leqslant\frac{7}{4}$时，$\angle MOC=\angle AOC+\angle AOM=75^{\circ}+(60t)^{\circ}=105^{\circ}$，解得$t=\frac{1}{2}$；
当$\frac{7}{4}\lt t\leqslant3$时，$\angle MOC=\angle BOC+\angle BOM=180^{\circ}-\angle AOC + 180^{\circ}-\angle AOM=360^{\circ}-75^{\circ}-(60t)^{\circ}=105^{\circ}$，解得$t = 3$.
综上所述，当$OM$旋转$\frac{1}{2}$秒或 3 秒时，$\angle MOC = 105^{\circ}$.

18（10分）[2024江苏南京调研]我们在解题时，经常会遇到“数的平方”，那么你有简便方法吗？这里，我们以“两位数的平方”为例，请你细心观察下列各式，探究其中的规律，回答问题：
$13^{2}=(13 + 3)\times10+3^{2}=169$，
$25^{2}=(25 + 5)\times20+5^{2}=625$，
$34^{2}=(34 + 4)\times30+4^{2}=1156$，
$62^{2}=(62 + 2)\times60+2^{2}=3844$，
……
（1）请根据上述规律填空：$41^{2}=$________ = ________；
（2）我们知道，任何一个两位数都可以表示为$10a + b$（个位数字b为小于10的自然数，十位数字a为小于10的正整数），根据上述规律写出：$(10a + b)^{2}=$________，并给出理由.

答案： 18. 【解】
(1)$41^{2}=(41 + 1)×40+1^{2}=1681$. 故答案为$(41 + 1)×40+1^{2}$，$1681$.
(2)$(10a + b)^{2}=(10a + b + b)×10a + b^{2}$.
理由：因为$(10a + b)^{2}=(10a)^{2}+2×10a×b + b^{2}=100a^{2}+20ab + b^{2}$，$(10a + b + b)×10a + b^{2}=100a^{2}+20ab + b^{2}$，所以$(10a + b)^{2}=(10a + b + b)×10a + b^{2}$. 故答案为$(10a + b + b)×10a + b^{2}$.

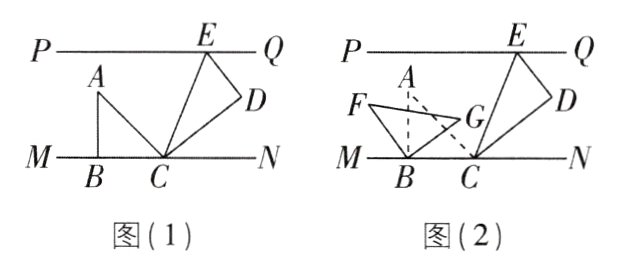
19（10分）[2024江苏宿迁期末]如图，直线$PQ// MN$，一副三角板（$\angle ABC=\angle CDE = 90^{\circ}$，$\angle ACB=\angle A = 45^{\circ}$，$\angle DEC = 60^{\circ}$，$\angle DCE = 30^{\circ}$）按图（1）所示方式放置，其中点E在直线PQ上，点B，C均在直线MN上，且CE平分$\angle ACN$.
（1）求$\angle DEQ$的度数.
（2）如图（2），将$\triangle ABC$绕点B以每秒$3^{\circ}$的速度按逆时针方向旋转（A，C的对应点分别为F，G），设旋转时间为$t\ s(0\leqslant t\leqslant60)$.
①在旋转过程中，若边$BG// CD$，求t的值.
②若在$\triangle ABC$绕点B旋转的同时，$\triangle CDE$绕点E以每秒$2^{\circ}$的速度按顺时针方向旋转（C，D的对应点为H，K）. 当边FG与$\triangle HKE$的一边平行时，请画出相应图形并写出对应的t值.

答案：
19. 【解】
(1)因为$\angle ACB = 45^{\circ}$，所以$\angle ACN = 135^{\circ}$. 因为$CE$平分$\angle ACN$，所以$\angle ECN = 67.5^{\circ}$. 因为$PQ// MN$，所以$\angle QEC = 180^{\circ}-\angle ECN = 180^{\circ}-67.5^{\circ}=112.5^{\circ}$. 因为$\angle DEC = 60^{\circ}$，所以$\angle DEQ=\angle QEC-\angle DEC = 112.5^{\circ}-60^{\circ}=52.5^{\circ}$.
(2)①因为$\angle DCE = 30^{\circ}$，$\angle ECN = 67.5^{\circ}$，所以$\angle DCN = 67.5^{\circ}-30^{\circ}=37.5^{\circ}$. 因为$BG// CD$，所以$\angle CBG=\angle DCN$，所以$3t^{\circ}=37.5^{\circ}$，所以$t = 12.5$.
②当$FG// HK$时，ⅰ. 如图
(1)所示，延长$FG$至点$L$，延长$BG$交$HE$于点$I$，交$PQ$于点$J$，交$HK$于点$O$，所以$\angle JGL=\angle FGB = 45^{\circ}$. 因为$FG// HK$，所以$\angle JOK=\angle JGL = 45^{\circ}$. 因为$\angle EHK = 30^{\circ}$，所以$\angle HIO = 180^{\circ}-\angle EHK-\angle IOH=\angle JOK-\angle EHK = 15^{\circ}$，所以$\angle JIE = 15^{\circ}$. 由题可知$\angle QEK = 52.5^{\circ}+2t^{\circ}$，所以$\angle JEI = 180^{\circ}-(52.5^{\circ}+2t^{\circ}+60^{\circ})$，所以$\angle PJB = 180^{\circ}-\angle BJE=\angle JEI+\angle JIE = 180^{\circ}-(52.5^{\circ}+2t^{\circ}+60^{\circ})+15^{\circ}$. 又因为$PQ// MN$，所以$\angle PJB=\angle GBN = 3t^{\circ}$，所以$180^{\circ}-(52.5^{\circ}+2t^{\circ}+60^{\circ})+15^{\circ}=3t^{\circ}$，解得$t = 16.5$.

ⅱ. 如图
(2)所示，延长$FG$交$PQ$于点$O$，设$HK$交$PQ$于点$L$，$GF$交$MN$于点$I$.
因为$\angle QEK = 52.5^{\circ}+2t^{\circ}$，所以$\angle PEK = 180^{\circ}-(52.5^{\circ}+2t^{\circ})$，所以$\angle PLK = 180^{\circ}-\angle KLQ=\angle K+\angle PEK = 90^{\circ}+180^{\circ}-(52.5^{\circ}+2t^{\circ})$.
因为$\angle GBN = 3t^{\circ}$，$\angle BGF = 45^{\circ}$，所以$\angle GIB = 180^{\circ}-\angle GBI-\angle BGF=\angle GBN-\angle BGF = 3t^{\circ}-45^{\circ}$. 因为$FG// HK$，$PQ// MN$，所以$\angle PLK+\angle EOI = 180^{\circ}$，$\angle GIB+\angle EOI = 180^{\circ}$，所以$\angle PLK=\angle GIB$，所以$90^{\circ}+180^{\circ}-(52.5^{\circ}+2t^{\circ})=3t^{\circ}-45^{\circ}$，解得$t = 52.5$.
当$FG// EK$时，如图
(3)所示，延长$EK$交$MN$于点$R$，设$FG$交$MN$于点$I$，则$GF// ER$. 因为$PQ// MN$，所以$\angle ERM=\angle QEK = 52.5^{\circ}+2t^{\circ}$. 又因为$GF// ER$，所以$\angle GIM=\angle ERM = 52.5^{\circ}+2t^{\circ}$. 因为$\angle GBN = 3t^{\circ}$，所以$\angle GBI = 180^{\circ}-3t^{\circ}$，所以$\angle GIM = 180^{\circ}-\angle BIG=\angle G+\angle GBI = 45^{\circ}+180^{\circ}-3t^{\circ}=52.5^{\circ}+2t^{\circ}$，解得$t = 34.5$.

当$FG// HE$时，ⅰ. 如图
(4)所示，延长$FG$，$BG$分别交$PQ$于点$S$，$T$. 因为$PQ// MN$，$\angle NBG = 3t^{\circ}$，所以$\angle BTS = 180^{\circ}-\angle NBG = 180^{\circ}-3t^{\circ}$. 又因为$HE// FS$，$\angle QEK = 52.5^{\circ}+2t^{\circ}$，所以$\angle FSP=\angle HEP = 180^{\circ}-(52.5^{\circ}+2t^{\circ})-60^{\circ}=67.5^{\circ}-2t^{\circ}$. 又因为$\angle TGS=\angle BGF = 45^{\circ}$，$\angle TGS+\angle GTS+\angle TSG = 180^{\circ}$，所以$45^{\circ}+180^{\circ}-3t^{\circ}+67.5^{\circ}-2t^{\circ}=180^{\circ}$，解得$t = 22.5$.

ⅱ. 如图
(5)所示，延长$HE$交$MN$于点$U$，设$FG$交$MN$于点$I$.
因为$\angle QEK = 52.5^{\circ}+2t^{\circ}$，所以$\angle QEU=\angle QEK-\angle KEU = 52.5^{\circ}+2t^{\circ}-(180^{\circ}-60^{\circ})=2t^{\circ}-67.5^{\circ}$.
因为$\angle GBN = 3t^{\circ}$，所以$\angle GBI = 180^{\circ}-\angle GBN = 180^{\circ}-3t^{\circ}$，所以$\angle GIM = 180^{\circ}-\angle GIB=\angle G+\angle GBI = 45^{\circ}+180^{\circ}-3t^{\circ}$.
又因为$PQ// MN$，$HU// FG$，所以$\angle GIM=\angle EUM=\angle QEU$，即$2t^{\circ}-67.5^{\circ}=45^{\circ}+180^{\circ}-3t^{\circ}$，解得$t = 58.5$.
综上所述，$t$的值为$16.5$，$22.5$，$34.5$，$52.5$，$58.5$.