第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
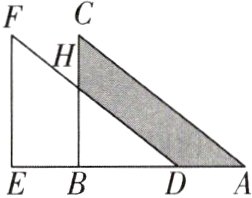
7[2024江苏无锡调研]如图,将△ABC沿射线AB方向平移4个单位长度得到△DEF,DF与BC交于点H,CH = 3,EF = 7.下列结论:①BH//EF;②AD = BD;③∠C = ∠BHD;④阴影部分的面积为22.其中一定正确的有________.(填序号)

答案:
①③④ 【解析】因为△ABC沿射线AB方向平移4个单位长度得到△DEF,所以$S_{\triangle ABC} = S_{\triangle DEF}$,BC//EF,AC//DF,BC = EF = 7,AD = BE = 4,故①正确,②不一定正确。因为AC//DF,所以∠C = ∠BHD,故③正确。因为$S_{阴影部分} + S_{\triangle BDH} = S_{梯形BEFH} + S_{\triangle BDH}$,所以$S_{阴影部分} = S_{梯形BEFH} = \frac{1}{2}×(4 + 7)×4 = 22$,故④正确。故答案为①③④。
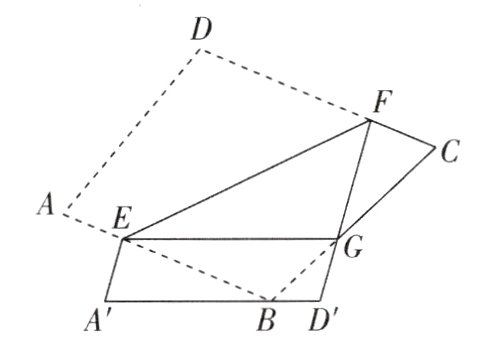
8[2024江苏无锡期中]如图,在四边形纸片ABCD中,AB//CD,将纸片沿EF折叠,点A,D 分别落在A',D'处,且A'D'经过点B,FD'交BC 于点G,连接EG,EG平分∠BEF.若EG//A'D',∠A + ∠DFE = 125°,则∠CFE的度数是________°.

答案:
130 【解析】设∠GEF = α。因为EG平分∠BEF,所以∠GEB = ∠GEF = α,∠BEF = 2∠GEF = 2α,所以∠AEF = 180° - ∠BEF = 180° - 2α。由折叠的性质得∠A'EF = ∠AEF = 180° - 2α,∠A = ∠A',所以∠A'EG = ∠A'EF - ∠GEF = 180° - 2α - α = 180° - 3α。因为AB//CD,所以∠DFE = ∠BEF = 2α。因为∠A + ∠DFE = 125°,所以∠A = 125° - ∠DFE = 125° - 2α,所以∠A' = ∠A = 125° - 2α。因为EG//A'D',所以∠A' + ∠A'EG = 180°,即125° - 2α + 180° - 3α = 180°,解得α = 25°,所以∠DFE = 2α = 50°,所以∠CFE = 180° - ∠DFE = 130°。故答案为130。
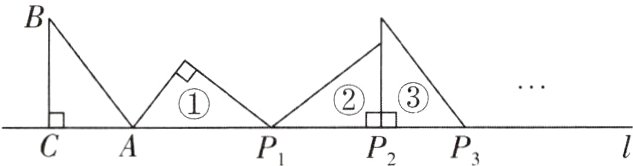
9新考法[2024广东深圳期中]如图,直角三角形ABC中,AC = 3,BC = 4,AB = 5,点C,A在直线l上,将△ABC绕点A顺时针旋转到位置①,得到点P1,点P1在直线l上,将位置①的三角形绕点P1顺时针旋转到位置②,得到点P2,点P2在直线l上,...,按照此规律继续旋转,直到得到点P2021,则AP2021 = __________.

答案:
8085 【解析】在直角三角形ABC中,因为∠ACB = 90°,AC = 3,BC = 4,AB = 5,所以将△ABC绕点A顺时针旋转到位置①,得到点P₁,此时AP₁ = 5;将位置①的三角形绕点P₁顺时针旋转到位置②,得到点P₂,此时AP₂ = 5 + 4 = 9;将位置②的三角形绕点P₂顺时针旋转到位置③,得到点P₃,此时AP₃ = 5 + 4 + 3 = 12。又因为2021÷3 = 673……2,所以AP₂₀₂₁ = 673×12 + (5 + 4) = 8085。故答案为8085。
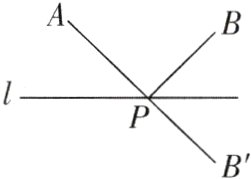
10[2024浙江杭州质检]如图,点A,B在直线l 的同侧,点B'是点B关于直线l的对称点,AB'交l于点P.
(1)AB'与AP+PB相等吗?为什么?
(2)在l上再取一点Q,并连接AQ和QB,比较AQ+QB与AP+PB的大小,并说明理由.
(1)AB'与AP+PB相等吗?为什么?
(2)在l上再取一点Q,并连接AQ和QB,比较AQ+QB与AP+PB的大小,并说明理由.

答案:
【解】
(1)AB'与AP + PB相等。理由如下:
连接BB',如图
(1)所示。
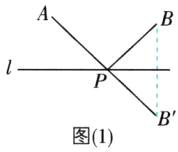
因为点B'是点B关于直线l的对称点,所以PB = PB',所以AP + PB' = AP + BP,即AB' = AP + BP。
(2)AQ + QB > AP + PB。理由如下:
如图
(2)所示,连接QB'。
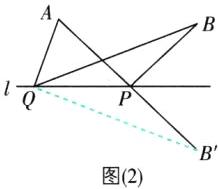
因为点B'是点B关于l的对称点,所以BQ = QB'。
因为AQ + QB' > AB',所以AQ + QB > AB'。
因为AB' = AP + PB,所以AQ + QB > AP + PB。
【解】
(1)AB'与AP + PB相等。理由如下:
连接BB',如图
(1)所示。

因为点B'是点B关于直线l的对称点,所以PB = PB',所以AP + PB' = AP + BP,即AB' = AP + BP。
(2)AQ + QB > AP + PB。理由如下:
如图
(2)所示,连接QB'。

因为点B'是点B关于l的对称点,所以BQ = QB'。
因为AQ + QB' > AB',所以AQ + QB > AB'。
因为AB' = AP + PB,所以AQ + QB > AP + PB。
11[2024江苏盐城期末]将三角板ABC与三角板ADE按图(1)所示方式摆放在一起,其中∠ACB = 30°,∠DAE = 45°,∠BAC = ∠D = 90°.
如图(2),固定三角板ABC,将三角板ADE绕点A按顺时针方向旋转,记旋转角∠CAE = α(0°<α<180°).
E固定三角板ABC D 三角板ADE绕点A
三角板ADE绕点A
按顺时针方向旋转B 图(2)
(1)在旋转过程中,当α为________时,AD//BC,当α为________时,AD⊥BC;
(2)当△ADE的一边与△ABC的某一边平行(不共线)时,直接写出旋转角α的所有可能的度数;
(3)当0°<α<45°时,连接BD,利用图(3)探究∠BDE + ∠CAE + ∠DBC的大小变化情况,并说明理由.


如图(2),固定三角板ABC,将三角板ADE绕点A按顺时针方向旋转,记旋转角∠CAE = α(0°<α<180°).
E固定三角板ABC D
 三角板ADE绕点A
三角板ADE绕点A 按顺时针方向旋转B 图(2)
(1)在旋转过程中,当α为________时,AD//BC,当α为________时,AD⊥BC;
(2)当△ADE的一边与△ABC的某一边平行(不共线)时,直接写出旋转角α的所有可能的度数;
(3)当0°<α<45°时,连接BD,利用图(3)探究∠BDE + ∠CAE + ∠DBC的大小变化情况,并说明理由.


答案:
【解】
(1)如图
(1),记DE与AC的交点为F,DE与BC的交点为G。
因为AD//BC,所以∠DAF = ∠C = 30°。
因为∠DAE = 45°,所以∠CAE = 15°,即α = 15°。
如图
(2),记AD与BC的交点为F。
因为AD⊥BC,所以∠AFC = 90°,
所以∠DAC = 180° - ∠AFC - ∠C = 180° - 90° - 30° = 60°,
所以∠CAE = ∠DAC + ∠EAD = 60° + 45° = 105°,即α = 105°。
故答案为15°,105°。
易错警示:
(2)题中并未说明△ADE与△ABC中具体哪两边平行,故需分情况讨论,注意不要漏解。
关键点拨:
(2)掌握轴对称的性质和两点之间线段最短是解答本题的关键。
(2)旋转角$\alpha$的所有可能的度数是$15^{\circ},45^{\circ},105^{\circ},135^{\circ},150^{\circ}$。
①当$AD// BC$时,如图
(1)所示,
由
(1)得,$\alpha = 15^{\circ}$;
②当$DE// BC$时,如图
(2)所示。
由
(1)得,$AD\perp BC$,所以$\angle AFB = 90^{\circ}$。
因为$\angle ADE = 90^{\circ}$,所以$DE// BC$,
所以$\alpha = 105^{\circ}$;
③当$DE// AB$时,如图
(3)所示,易知$\alpha = 45^{\circ}$;
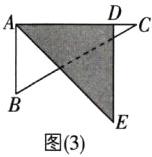
④当$DE// AC$时,如图
(4)所示,
$\alpha=\angle EAD+\angle BAC = 45^{\circ}+90^{\circ}=135^{\circ}$;
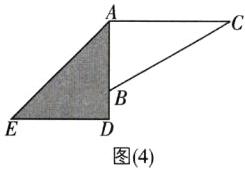
⑤当$AE// BC$时,如图
(5)所示,$\angle EAC+\angle C = 180^{\circ}$。
因为$\angle C = 30^{\circ}$,所以$\angle EAC = 150^{\circ}$,即$\alpha = 150^{\circ}$。
综上所述,旋转角$\alpha$的所有可能的度数是$15^{\circ},45^{\circ},105^{\circ},135^{\circ},150^{\circ}$。
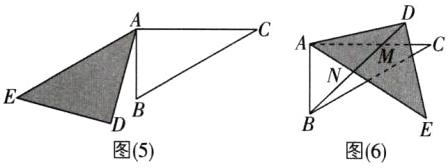
(3)当$0^{\circ}<\alpha<45^{\circ}$时,$\angle BDE+\angle CAE+\angle DBC = 105^{\circ}$,保持不变,理由如下:如图
(6),设$BD$分别交$AC$,$AE$于点$M$,$N$。在$\triangle AMN$中,$\angle AMN+\angle CAE+\angle ANM = 180^{\circ}$。
因为$\angle ANM=\angle E+\angle BDE$,$\angle AMN=\angle C+\angle DBC$,所以$\angle E+\angle BDE+\angle CAE+\angle C+\angle DBC = 180^{\circ}$。
因为$\angle C = 30^{\circ}$,$\angle E = 45^{\circ}$,
所以$\angle BDE+\angle CAE+\angle DBC = 105^{\circ}$。
【解】
(1)如图
(1),记DE与AC的交点为F,DE与BC的交点为G。
因为AD//BC,所以∠DAF = ∠C = 30°。
因为∠DAE = 45°,所以∠CAE = 15°,即α = 15°。
如图
(2),记AD与BC的交点为F。
因为AD⊥BC,所以∠AFC = 90°,
所以∠DAC = 180° - ∠AFC - ∠C = 180° - 90° - 30° = 60°,
所以∠CAE = ∠DAC + ∠EAD = 60° + 45° = 105°,即α = 105°。
故答案为15°,105°。
易错警示:
(2)题中并未说明△ADE与△ABC中具体哪两边平行,故需分情况讨论,注意不要漏解。
关键点拨:
(2)掌握轴对称的性质和两点之间线段最短是解答本题的关键。
(2)旋转角$\alpha$的所有可能的度数是$15^{\circ},45^{\circ},105^{\circ},135^{\circ},150^{\circ}$。
①当$AD// BC$时,如图
(1)所示,
由
(1)得,$\alpha = 15^{\circ}$;
②当$DE// BC$时,如图
(2)所示。
由
(1)得,$AD\perp BC$,所以$\angle AFB = 90^{\circ}$。
因为$\angle ADE = 90^{\circ}$,所以$DE// BC$,
所以$\alpha = 105^{\circ}$;
③当$DE// AB$时,如图
(3)所示,易知$\alpha = 45^{\circ}$;

④当$DE// AC$时,如图
(4)所示,
$\alpha=\angle EAD+\angle BAC = 45^{\circ}+90^{\circ}=135^{\circ}$;

⑤当$AE// BC$时,如图
(5)所示,$\angle EAC+\angle C = 180^{\circ}$。
因为$\angle C = 30^{\circ}$,所以$\angle EAC = 150^{\circ}$,即$\alpha = 150^{\circ}$。
综上所述,旋转角$\alpha$的所有可能的度数是$15^{\circ},45^{\circ},105^{\circ},135^{\circ},150^{\circ}$。

(3)当$0^{\circ}<\alpha<45^{\circ}$时,$\angle BDE+\angle CAE+\angle DBC = 105^{\circ}$,保持不变,理由如下:如图
(6),设$BD$分别交$AC$,$AE$于点$M$,$N$。在$\triangle AMN$中,$\angle AMN+\angle CAE+\angle ANM = 180^{\circ}$。
因为$\angle ANM=\angle E+\angle BDE$,$\angle AMN=\angle C+\angle DBC$,所以$\angle E+\angle BDE+\angle CAE+\angle C+\angle DBC = 180^{\circ}$。
因为$\angle C = 30^{\circ}$,$\angle E = 45^{\circ}$,
所以$\angle BDE+\angle CAE+\angle DBC = 105^{\circ}$。
查看更多完整答案,请扫码查看


