《2025年初中必刷题七年级数学下册苏科版》

1[中]学校一长方形草地中需修建一条等宽的小路，为了达到“曲径通幽”的效果，有下列四种设计方案，其中有一种方案修建小路后剩余草坪面积与其他三种方案不等，它是 （ ）

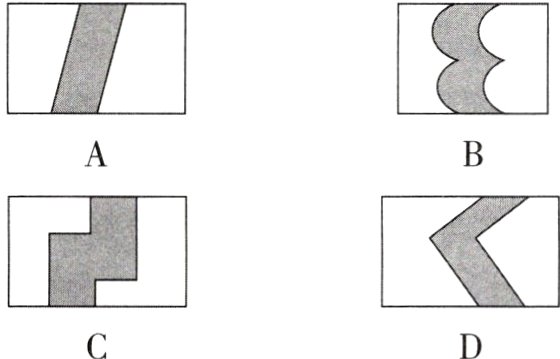
A B C D

答案： C【解析】A，B，D三种方案剩余草坪面积都是(长方形的长 - 小路的宽)×长方形的宽，而C方案的小路的面积比其他三种方案多1个以小路的宽度为边长的正方形的面积。故选C。

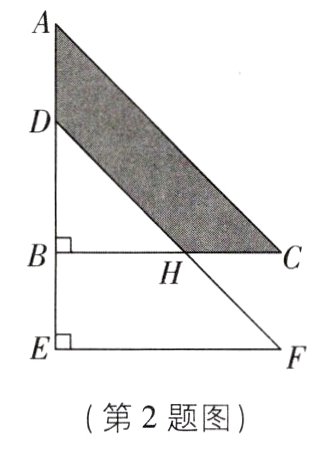
2[2024江苏江阴期末，中]如图，将直角三角形ABC沿AB方向平移2 cm得到△DEF，DF交BC于点H，CH = 2 cm，EF = 5 cm，则阴影部分的面积为 （ ）

A. 6 cm²
B. 8 cm²
C. 12 cm²
D. 16 cm²

答案： B【解析】由平移的性质可知，$BC = EF = 5\ cm$，$AD = BE = 2\ cm$，$\angle E=\angle ABC = 90^{\circ}$，$S_{\triangle ABC}=S_{\triangle DEF}$，所以$BH = BC - CH = 5 - 2 = 3(cm)$。因为$S_{\triangle ABC}=S_{阴影}+S_{\triangle DBH}$，$S_{\triangle DEF}=S_{梯形BEFH}+S_{\triangle DBH}$，所以$S_{阴影}+S_{\triangle DBH}=S_{梯形BEFH}+S_{\triangle DBH}$，所以$S_{阴影}=S_{梯形BEFH}$，所以$S_{阴影}=S_{梯形BEFH}=\frac{1}{2}(BH + EF)\cdot BE=\frac{1}{2}\times(3 + 5)\times2 = 8(cm^{2})$。故选B。

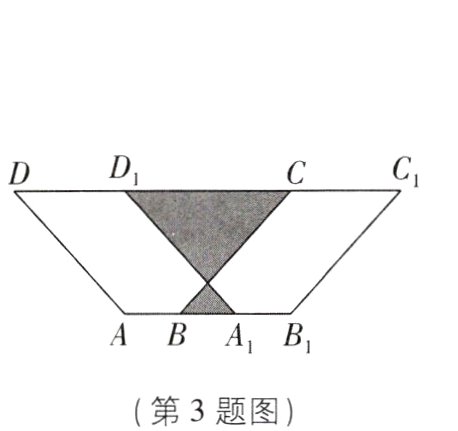
3[2024重庆期中，中]如图，梯形ABCD沿AB方向平移2个单位长度得到梯形A₁B₁C₁D₁，连接A₁B. 若AB = 1，CD = 5，AD = BC = 3，则图中阴影部分的周长为________.

答案： 10【解析】由平移的性质可得$AA_{1}=DD_{1}=2$，$A_{1}D_{1}=AD = 3$，所以$CD_{1}=CD - DD_{1}=3$，$A_{1}B = AA_{1}-AB = 1$，所以题图中阴影部分的周长为$BC + A_{1}D_{1}+CD_{1}+A_{1}B = 3 + 3 + 3 + 1 = 10$。故答案为10。

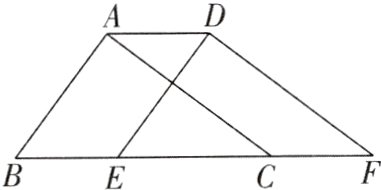
4[2024浙江杭州期末，中]如图，在三角形ABC中，∠BAC = 90°，AB = 3，AC = 4，BC = 5，将三角形ABC沿直线BC向右平移2个单位得到三角形DEF，连接AD，则下列结论：①AC//DF，AC = DF；②ED⊥AC；③四边形ABFD的周长是16；④AD:EC = 2:3，其中正确结论有________（填序号）.

答案： ①②③④【解析】由平移可知，$AC//DF$，$AC = DF$，故①正确。由平移可知，$\angle EDF=\angle BAC = 90^{\circ}$，即$ED\perp DF$。又因为$AC//DF$，所以$ED\perp AC$，故②正确。由平移可知，$AD = CF = 2$，$DF = AC = 4$，所以$C_{四边形ABFD}=AB + BF + FD + DA = 3 + 5 + 2 + 4 + 2 = 16$，故③正确。由平移可知，$BE = 2$。因为$BC = 5$，所以$EC = 3$。又因为$AD = 2$，所以$AD:EC = 2:3$，故④正确。故答案为①②③④。

5[2024江苏泰州期末，较难]如图，在锐角△ABC中，∠BAC = 60°，将△ABC沿着射线BC方向平移得到△A'B'C'（平移后点A，B，C的对应点分别是点A'，B'，C'），连接CA'，若在整个平移过程中，∠ACA'和∠CA'B'的度数之间存在2倍关系，则∠ACA'的度数为________.

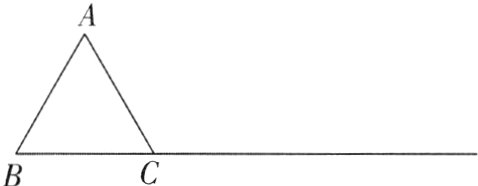
答案：
$20^{\circ}$或$40^{\circ}$或$120^{\circ}$【解析】第一种情况：如图
(1)，当点$B'$在边BC上时，过点C作$CG//AB$。

因为$\triangle A'B'C'$由$\triangle ABC$平移得到，所以$AB//A'B'$。因为$CG//AB$，$AB//A'B'$，所以$CG//AB//A'B'$。①当$\angle ACA' = 2\angle CA'B'$时，设$\angle CA'B' = x$，则$\angle ACA' = 2x$。因为$CG//AB//A'B'$，所以$\angle ACG=\angle BAC = 60^{\circ}$，$\angle A'CG=\angle CA'B' = x$。因为$\angle ACG=\angle ACA'+\angle A'CG$，所以$2x + x = 60^{\circ}$，解得$x = 20^{\circ}$，所以$\angle ACA' = 2x = 40^{\circ}$。②当
本题主要考查了平移的性质，将阴影部分的面积转化为规则图形的面积是解题的关键。
思路分析：根据$\triangle ABC$的平移过程，分点$B'$在边BC上和在边BC的延长线上两种情况。作$CG//AB$，根据平移得到$CG//AB//A'B'$，再根据平行线的性质及角的和差关系列方程求解。
$\angle CA'B' = 2\angle ACA'$时，设$\angle CA'B' = x$，则$\angle ACA'=\frac{1}{2}x$，$\angle A'CG=\angle CA'B' = x$。因为$\angle ACG=\angle ACA'+\angle A'CG$，所以$\frac{1}{2}x + x = 60^{\circ}$，解得$x = 40^{\circ}$，所以$\angle ACA'=\frac{1}{2}x = 20^{\circ}$。
第二种情况：如图
(2)，当点$B'$在边BC的延长线上时，过点C作$CG//AB$。

因为$\triangle A'B'C'$由$\triangle ABC$平移得到，所以$AB//A'B'$。因为$CG//AB$，$AB//A'B'$，所以$CG//AB//A'B'$。①当$\angle ACA' = 2\angle CA'B'$时，设$\angle CA'B' = x$，则$\angle ACA' = 2x$。因为$CG//AB//A'B'$，所以$\angle ACG=\angle BAC = 60^{\circ}$，$\angle A'CG=\angle CA'B' = x$。因为$\angle ACA'=\angle ACG+\angle A'CG$，所以$2x = 60^{\circ}+x$，解得$x = 60^{\circ}$，所以$\angle ACA' = 2x = 120^{\circ}$。②当$\angle CA'B' = 2\angle ACA'$时，分析图形可知，$\angle CA'B'＜\angle ACA'$，故不存在这种情况。综上所述，$\angle ACA'$的度数为$20^{\circ}$或$40^{\circ}$或$120^{\circ}$。

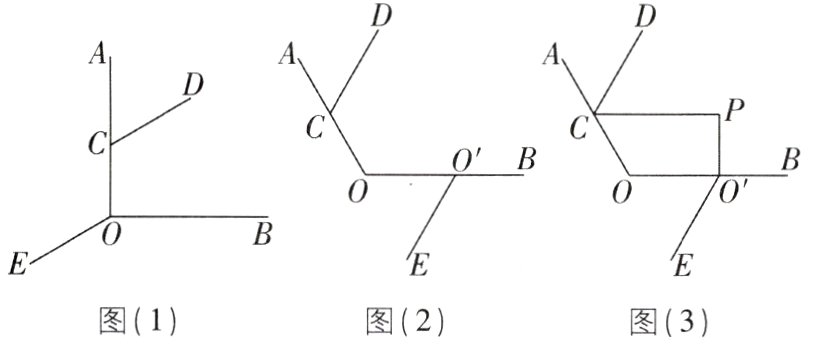
6核心素养 几何直观[较难]已知∠AOB = 90°，点C在射线OA上，CD//OE.
(1)如图(1)，若∠OCD = 120°，求∠BOE的度数；
(2)把“∠AOB = 90°”改为“∠AOB = 120°”，将射线OE沿射线OB平移得到O'E，其他条件不变，如图(2)所示，探究∠OCD与∠BO'E之间的数量关系；
(3)在(2)的条件下，作PO'⊥OB，垂足为O'，与∠OCD的平分线CP交于点P，如图(3)所示，若∠BO'E = α，请用含α的式子表示∠CPO'（请直接写出答案）.

答案：
【解】
(1)因为$CD//OE$，所以$\angle AOE=\angle OCD = 120^{\circ}$，所以$\angle BOE = 360^{\circ}-90^{\circ}-120^{\circ}=150^{\circ}$。
(2)如图，过O点作$OF//CD$。

由题意得$CD//O'E$，所以$CD//OF//O'E$，所以$\angle AOF = 180^{\circ}-\angle OCD$，$\angle BOF=\angle EO'O = 180^{\circ}-\angle BO'E$，所以$\angle AOB=\angle AOF+\angle BOF = 180^{\circ}-\angle OCD + 180^{\circ}-\angle BO'E = 360^{\circ}-(\angle OCD+\angle BO'E)=120^{\circ}$，所以$\angle OCD+\angle BO'E = 240^{\circ}$。
(3)$\angle CPO' = 30^{\circ}+\frac{1}{2}\alpha$。
因为CP是$\angle OCD$的平分线，所以$\angle OCP=\frac{1}{2}\angle OCD$，所以$\angle CPO' = 360^{\circ}-90^{\circ}-120^{\circ}-\angle OCP = 150^{\circ}-\frac{1}{2}\angle OCD = 150^{\circ}-\frac{1}{2}(240^{\circ}-\angle BO'E)=30^{\circ}+\frac{1}{2}\alpha$。