《2025年初中必刷题七年级数学下册苏科版》

1[2024江苏无锡期中,中]某污水处理厂现有待处理的污水m吨,另有从城区流入的待处理污水(新流入污水按每小时n吨的定流量增加).若该厂同时开动2台机组,需30小时处理完污水;若同时开动3台机组,需15小时处理完污水.若5小时处理完污水,则需同时开动机组(　　　)
A. 6台　　
　B. 7台　
　C. 8台　
　D. 9台

答案： B 【解析】设同时开动$x$台机组，每台机组每小时处理$a$吨污水. 依题意，得$\begin{cases}2\times30a = m + 30n,\\3\times15a = m + 15n,\end{cases}$
解得$\begin{cases}m = 30a,\\n = a.\end{cases}$所以$5ax = m + 5n = 30a + 5a$，所以$x = 7$. 所以若$5$小时处理完污水，则需同时开动$7$台机组. 故选 B.

2[2024江苏宿迁期末,较难]甲、乙、丙三人在A,B两块地植树,其中甲在A地植树,丙在B 地植树,乙先在A地植树,然后转到B地.已知甲、乙、丙每小时分别能植树10棵、8棵、12棵.若乙在A地植树12小时后立即转到B地,则两块地同时开始同时结束;若要两块地同时开始,但A地比B地早6小时结束,则乙应在A地植树________小时后立即转到B地.

答案： 17 【解析】设$A$地需要植树$x$棵，$B$地需要植树$y$棵. 由题可得，$\frac{x - 12(10 + 8)}{10}=\frac{y - 12\times12}{12 + 8}$.
若要两块地同时开始，但$A$地比$B$地早$6$小时结束，则设乙应在$A$地植树$t$小时后立即转到$B$地. 由题可得，$\frac{x - t(10 + 8)}{10}+6=\frac{y - 12t}{12 + 8}$，则
可列出方程组$\begin{cases}\frac{x - 12(10 + 8)}{10}=\frac{y - 12\times12}{12 + 8},①\\\frac{x - t(10 + 8)}{10}+6=\frac{y - 12t}{12 + 8},②\end{cases}$由
$①$整理得$y = 2x - 288$，代入$②$中化简得$2x - 36t + 120 = 2x - 288 - 12t$，解得$t = 17$. 故答案为$17$.

3[2024江苏南京质检,中]一项工程,甲队单独做需12天完成,乙队单独做需15天完成,丙队单独做需20天完成.按原计划,这项工程要在7 天内完成,现甲、乙两队先合作若干天,后为加快进度,丙队加入这项工程,这样比原计划提前一天完成,求甲、乙两队合作了多少天.

答案： 【解】设甲、乙两队合作了$x$天，丙队加入后又做了$y$天.
根据题意，得$\begin{cases}x + y = 7 - 1,\\(\frac{1}{12}+\frac{1}{15})x+(\frac{1}{12}+\frac{1}{15}+\frac{1}{20})y = 1,\end{cases}$
解得$\begin{cases}x = 4,\\y = 2.\end{cases}$
答：甲、乙两队合作了$4$天.

4[2024重庆北碚区期末,中]如图所示,D,E分别为三角形ABC的边AB,AC上两点,将三角形ABC沿DE折叠,点A落在BC边上的点F处，连接AF,∠BDF = ∠FEC - 20°,9∠BDF = 8 ∠BAC,求∠BAC的度数.
　　　　　　　　　　　

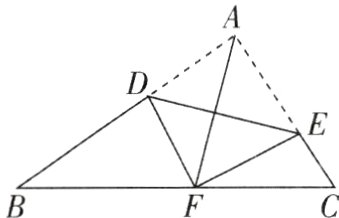
答案： 【解】设$\angle FEC = x^{\circ}$，$\angle BAC = y^{\circ}$. 由折叠知$\angle BAC = \angle DFE$，所以$\angle BDF+\angle FEC = 180^{\circ}-\angle B-\angle DFB + 180^{\circ}-\angle C-\angle EFC = 360^{\circ}-(\angle B+\angle C+\angle DFB+\angle EFC)=360^{\circ}-(180^{\circ}-\angle BAC + 180^{\circ}-\angle DFE)=2\angle BAC$，则可列方程组$\begin{cases}x - 20 + x = 2y,\\9(x - 20)=8y,\end{cases}$解得$\begin{cases}x = 100,\\y = 90,\end{cases}$即$\angle BAC = 90^{\circ}$.

5[2024浙江杭州期中,中]如图是边长为1个单位长度的小正方形组成的网格.
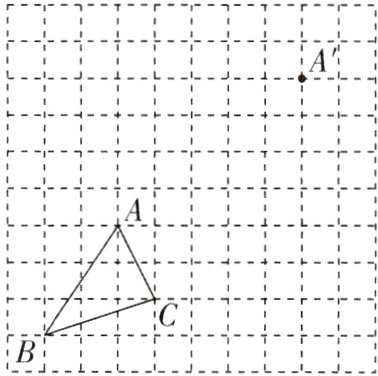
(1)把三角形ABC进行平移，得到三角形A'B'C',使点A与A'对应,请在网格中画出三角形A'B'C'.
(2)将一个格点多边形(顶点均在格点上)的面积记为S,其内部格点数记为N,边界上的格点数记为L
①图中格点三角形ABC对应的N = ________，L = ________，S = ________.
②已知格点多边形的面积可表示为S = N + aL + b,且已知当N = 1,L = 6时,S = 3.若某格点多边形对应的N = 12,L = 8,求S的值.
　　　　　　　　　　

答案：
【解】
(1)如图所示，三角形$A'B'C'$即为所作.
(2)①由图可知$N = 3$，$L = 3$，$S = 3\times3-\frac{1}{2}\times3\times1-\frac{1}{2}\times2\times1-\frac{1}{2}\times2\times3 = 3.5$. 故答案为$3$，$3$，$3.5$.
②由题意得$\begin{cases}3 + 3a + b = 3.5,\\1 + 6a + b = 3,\end{cases}$解得$\begin{cases}a=\frac{1}{2},\\b = - 1,\end{cases}$所以$S = N+\frac{1}{2}L - 1$，所以当$N = 12$，$L = 8$时，$S = 15$.