《2025年初中必刷题七年级数学下册苏科版》

1[2024山东泰安期中]下列计算错误的是（ ）
A. $3x^{2}\cdot2x^{3}=6x^{5}$
B. $-ac^{2}\cdot(-7ab^{2})=7ab^{2}c^{2}$
C. $5x^{2}y\cdot(-2xy^{5})=-10x^{3}y^{6}$
D. $34ax\cdot2by=68abxy$

答案： B
思路分析 单项式相乘的运算步骤：一定系数，系数的积作为积的系数；二定同底数幂，将同底数幂分别相乘；三定其余，只在一个单项式中出现的字母，连同指数作为积的一个因式。
思路分析：将原方程化为$2^{a + 2c}\cdot3^{b}=2^{6}\cdot3$，得到$a + 2c = 6$，$b = 1$，再根据$a$，$b$，$c$为自然数，求出$a$，$c$的值，进而求出答案。
易错警示：注意计算前把互为相反数的两个底数化成相同底数，再进行同底数幂的乘法，最后合并同类项。在计算单项式乘单项式时，不要漏掉只在一个单项式中出现的字母及其指数。
(2) 因为$3\times2^{x + 3}\times4^{x + 3}=96$，所以$2^{x + 3}\times4^{x + 3}=32$，所以$(2\times4)^{x + 3}=32$，即$8^{x + 3}=32$，所以$2^{3(x + 3)}=2^{5}$，所以$3(x + 3)=5$，解得$x = -\frac{4}{3}$。

2[2024江苏常州武进区质检]计算$8xy^{3}\cdot\left(-\frac{1}{4}x^{3}y^{2}\right)$的结果是（ ）
A. $2x^{4}y^{5}$
B. $-2x^{4}y^{5}$
C. $2x^{3}y^{6}$
D. $-2x^{3}y^{5}$

答案： B 【解析】$8xy^{3}\cdot(-\frac{1}{4}x^{3}y^{2})=-2x^{4}y^{5}$。故选 B。

3[2024江苏淮安淮阴区期中]已知单项式$3x^{2}y^{3}$与$-2xy^{2}$的积为$mx^{3}y^{n}$，则$m$，$n$的值为（ ）
A. $-6,6$
B. $-6,5$
C. $1,6$
D. $1,5$

答案： B 【解析】因为$3x^{2}y^{3}\times(-2xy^{2})=-6x^{3}y^{5}$，且单项式$3x^{2}y^{3}$与$-2xy^{2}$的积为$mx^{3}y^{n}$，所以$m = -6$，$n = 5$。故选 B。

4新考向开放性试题[2023江苏无锡新吴区期中]已知两个单项式的积是$-6a^{3}b^{2}$，这两个单项式可以是________（写出一对即可）.

答案： $-2a^{2}b$，$3ab$（答案不唯一）【解析】$-2a^{2}b\cdot3ab=-6a^{3}b^{2}$。故答案为$-2a^{2}b$，$3ab$（答案不唯一）。

5若单项式$-6x^{2}y^{m}$与$\frac{1}{2}x^{n - 1}y^{3}$是同类项，则这两个单项式的积是________.

答案： $-3x^{4}y^{6}$【解析】由题意得$n - 1 = 2$，$m = 3$，则$n = 3$，所以$-6x^{2}y^{3}\cdot\frac{1}{2}x^{2}y^{3}=-3x^{4}y^{6}$。故答案为$-3x^{4}y^{6}$。

6[2024江苏泰州质检]计算：
(1)$(-3a^{3})^{2}\cdot a^{3}+(-4a)^{2}\cdot a^{7}+(-5a^{3})^{3}$；
(2)$(-x)^{2}\cdot x^{3}\cdot(-2y)^{3}+(-2xy)^{2}\cdot(-x)^{3}y$.

答案： 【解】
(1) 原式$=9a^{6}\cdot a^{3}+16a^{2}\cdot a^{7}-125a^{9}=9a^{9}+16a^{9}-125a^{9}=-100a^{9}$。
(2) 原式$=x^{2}\cdot x^{3}\cdot(-8y^{3})+4x^{2}y^{2}\cdot(-x^{3})y=-8x^{5}y^{3}-4x^{5}y^{3}=-12x^{5}y^{3}$。

7[2024山东青岛质检]已知$-2x^{3m + 1}y^{2n}$与$4x^{-3}y^{4}$的积与$-4x^{4}y^{2}$是同类项.
(1)求$m$，$n$的值.
(2)先化简，再求值：$5m^{3}n\cdot(-3n)^{2}+(6mn)^{2}\cdot(-mn)-mn^{3}\cdot(-4m)^{2}$.

答案： 【解】
(1)$-2x^{3m + 1}y^{2n}\cdot4x^{-3}y^{4}=-8x^{3m + 1 - 3}y^{2n + 4}$。因为$-2x^{3m + 1}y^{2n}$与$4x^{-3}y^{4}$的积与$-4x^{4}y^{2}$是同类项，所以$-8x^{3m + 1 - 3}y^{2n + 4}$与$-4x^{4}y^{2}$是同类项，所以$3m + 1 - 3 = 4$，$2n + 4 = 2$，所以$m = 2$，$n = -1$。
(2)$5m^{3}n\cdot(-3n)^{2}+(6mn)^{2}\cdot(-mn)-mn^{3}\cdot(-4m)^{2}=5m^{3}n\cdot9n^{2}+36m^{2}n^{2}\cdot(-mn)-mn^{3}\cdot16m^{2}=45m^{3}n^{3}-36m^{3}n^{3}-16m^{3}n^{3}=-7m^{3}n^{3}$。当$m = 2$，$n = -1$时，原式$=-7\times2^{3}\times(-1)^{3}=56$。

8[2023湖北荆门质检]某商场四月份售出某品牌衬衣$b$件，每件$c$元，营业额$a$元. 五月份采取促销活动，售出该品牌衬衣$3b$件，每件打八折，则五月份该品牌衬衣的营业额比四月份增加（ ）
A. $1.4a$元
B. $2.4a$元
C. $3.4a$元
D. $4.4a$元

答案： A 【解析】由题意得四月份营业额为$bc = a$，五月份营业额为$3b\times\frac{4}{5}c=\frac{12}{5}bc=\frac{12}{5}a$，所以$\frac{12}{5}a - a = 1.4a$。故选 A。

9[2023湖南长沙雨花区调研]已知$A = 3x^{2}$，$B = -2xy^{2}$，$C = -x^{2}y^{2}$，则$A\cdot B^{2}\cdot C$的值为________.

答案： $-12x^{6}y^{6}$【解析】$A\cdot B^{2}\cdot C=(3x^{2})\cdot(-2xy^{2})^{2}\cdot(-x^{2}y^{2})=(3x^{2})\cdot(4x^{2}y^{4})\cdot(-x^{2}y^{2})=-12x^{6}y^{6}$。故答案为$-12x^{6}y^{6}$。

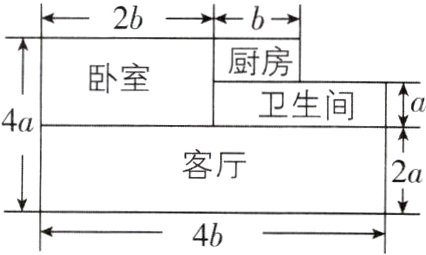
10[2024江苏无锡期中]张叔叔刚分到一套新房，其结构如图所示（单位：米）. 他打算除卧室外都铺上地砖.
(1)需要铺多少平方米地砖？
(2)如果铺的这种地砖的价格是每平方米$2m$元，那么铺地砖一共需要花多少钱？

答案： 【解】
(1) 根据题意，得除卧室外，其余部分的面积为$4a\times4b - ab - 2a\times2b = 11ab$（平方米）。答：需要铺$11ab$平方米地砖。
(2)$11ab\times2m = 22abm$（元）。答：铺地砖一共需要花$22abm$元。