第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
17[2024重庆北碚区期中]关于 $x$ 的代数式 $(ax - 3)(2x + 1)-4x^{2}+m$ 化简后不含有 $x^{2}$ 项和常数项,且 $an+mn = 1$,求 $2n^{3}-9n^{2}+8n$ 的值.
答案:
【解】$(ax - 3)(2x + 1)-4x^{2}+m=2ax^{2}+ax-6x-3-4x^{2}+m=(2a - 4)x^{2}+(a - 6)x+m - 3$. 因为化简后不含有 $x^{2}$ 项和常数项,所以 $2a - 4 = 0$,$m - 3 = 0$,所以 $a = 2$,$m = 3$. 因为 $an+mn = 1$,所以 $2n+3n = 1$,解得 $n=\frac{1}{5}$,所以 $2n^{3}-9n^{2}+8n=2\times(\frac{1}{5})^{3}-9\times(\frac{1}{5})^{2}+8\times\frac{1}{5}=\frac{2}{125}-\frac{9}{25}+\frac{8}{5}=\frac{157}{125}$.
18已知 $m - n = 4$,$mn = -3$.
(1)求 $m^{2}+n^{2}$ 的值;
(2)求 $(m^{2}-4)(n^{2}-4)$ 的值;
(3)求 $8^{m}\cdot32^{n}\div4^{m + 2n}$ 的值.
(1)求 $m^{2}+n^{2}$ 的值;
(2)求 $(m^{2}-4)(n^{2}-4)$ 的值;
(3)求 $8^{m}\cdot32^{n}\div4^{m + 2n}$ 的值.
答案:
【解】(1)因为 $m - n = 4$,$mn=-3$,所以 $m^{2}+n^{2}=(m - n)^{2}+2mn=4^{2}+2\times(-3)=16-6 = 10$.
(2)原式$=(mn)^{2}-4(m^{2}+n^{2})+16$. 当 $mn=-3$,$m^{2}+n^{2}=10$ 时,原式$=(-3)^{2}-4\times10+16=9-40+16=-15$.
(3)$8^{m}\cdot32^{n}\div4^{m + 2n}=(2^{3})^{m}\cdot(2^{5})^{n}\div(2^{2})^{m + 2n}=2^{3m}\cdot2^{5n}\div2^{2m + 4n}=2^{3m + 5n}\div2^{2m + 4n}=2^{3m + 5n-2m-4n}=2^{m + n}$. 因为 $m - n = 4$,$mn=-3$,所以 $(m + n)^{2}=(m - n)^{2}+4mn=4^{2}+4\times(-3)=16-12 = 4$,所以 $m + n = 2$ 或 -2,所以 $2^{m + n}=2^{2}=4$ 或 $2^{m + n}=2^{-2}=\frac{1}{4}$.
(2)原式$=(mn)^{2}-4(m^{2}+n^{2})+16$. 当 $mn=-3$,$m^{2}+n^{2}=10$ 时,原式$=(-3)^{2}-4\times10+16=9-40+16=-15$.
(3)$8^{m}\cdot32^{n}\div4^{m + 2n}=(2^{3})^{m}\cdot(2^{5})^{n}\div(2^{2})^{m + 2n}=2^{3m}\cdot2^{5n}\div2^{2m + 4n}=2^{3m + 5n}\div2^{2m + 4n}=2^{3m + 5n-2m-4n}=2^{m + n}$. 因为 $m - n = 4$,$mn=-3$,所以 $(m + n)^{2}=(m - n)^{2}+4mn=4^{2}+4\times(-3)=16-12 = 4$,所以 $m + n = 2$ 或 -2,所以 $2^{m + n}=2^{2}=4$ 或 $2^{m + n}=2^{-2}=\frac{1}{4}$.
19[2023江苏扬州广陵区期中]阅读材料:
若 $m^{2}-2mn + 2n^{2}-8n + 16 = 0$,求 $m$,$n$ 的值.
解:因为 $m^{2}-2mn + 2n^{2}-8n + 16 = 0$,所以 $(m^{2}-2mn + n^{2})+(n^{2}-8n + 16)=0$,
所以 $(m - n)^{2}+(n - 4)^{2}=0$,所以 $m - n = 0$,$n - 4 = 0$,所以 $n = 4$,$m = 4$.
根据你的观察,探究下面的问题:
(1)已知 $a^{2}+b^{2}-2a + 1 = 0$,则 $a =$________,$b =$________.
(2)已知 $x^{2}+2y^{2}-2xy + 6y + 9 = 0$,求 $x^{y}$ 的值.
(3)已知 $\triangle ABC$ 的三边长 $a$,$b$,$c$ 都是正整数,且满足 $2a^{2}+b^{2}-4a - 6b + 11 = 0$,求 $\triangle ABC$ 的周长.
若 $m^{2}-2mn + 2n^{2}-8n + 16 = 0$,求 $m$,$n$ 的值.
解:因为 $m^{2}-2mn + 2n^{2}-8n + 16 = 0$,所以 $(m^{2}-2mn + n^{2})+(n^{2}-8n + 16)=0$,
所以 $(m - n)^{2}+(n - 4)^{2}=0$,所以 $m - n = 0$,$n - 4 = 0$,所以 $n = 4$,$m = 4$.
根据你的观察,探究下面的问题:
(1)已知 $a^{2}+b^{2}-2a + 1 = 0$,则 $a =$________,$b =$________.
(2)已知 $x^{2}+2y^{2}-2xy + 6y + 9 = 0$,求 $x^{y}$ 的值.
(3)已知 $\triangle ABC$ 的三边长 $a$,$b$,$c$ 都是正整数,且满足 $2a^{2}+b^{2}-4a - 6b + 11 = 0$,求 $\triangle ABC$ 的周长.
答案:
【解】(1)因为 $a^{2}+b^{2}-2a + 1 = 0$,所以 $a^{2}-2a + 1+b^{2}=0$,所以 $(a - 1)^{2}+b^{2}=0$,所以 $a - 1 = 0$,$b = 0$,解得 $a = 1$,$b = 0$. 故答案为 1,0.
(2)因为 $x^{2}+2y^{2}-2xy + 6y + 9 = 0$,所以 $x^{2}+y^{2}-2xy+y^{2}+6y + 9 = 0$,所以 $(x - y)^{2}+(y + 3)^{2}=0$,所以 $x - y = 0$,$y + 3 = 0$,解得 $x = y=-3$,所以 $x^{y}=(-3)^{-3}=-\frac{1}{27}$.
(3)因为 $2a^{2}+b^{2}-4a-6b + 11 = 0$,所以 $2a^{2}-4a + 2+b^{2}-6b + 9 = 0$,所以 $2(a - 1)^{2}+(b - 3)^{2}=0$,所以 $a - 1 = 0$,$b - 3 = 0$,解得 $a = 1$,$b = 3$. 由三角形三边关系可知 $3 - 1<c<3 + 1$,所以 $2<c<4$. 又因为 $c$ 为正整数,所以 $c = 3$,所以 $\triangle ABC$ 的周长为 $1+3+3 = 7$.
(2)因为 $x^{2}+2y^{2}-2xy + 6y + 9 = 0$,所以 $x^{2}+y^{2}-2xy+y^{2}+6y + 9 = 0$,所以 $(x - y)^{2}+(y + 3)^{2}=0$,所以 $x - y = 0$,$y + 3 = 0$,解得 $x = y=-3$,所以 $x^{y}=(-3)^{-3}=-\frac{1}{27}$.
(3)因为 $2a^{2}+b^{2}-4a-6b + 11 = 0$,所以 $2a^{2}-4a + 2+b^{2}-6b + 9 = 0$,所以 $2(a - 1)^{2}+(b - 3)^{2}=0$,所以 $a - 1 = 0$,$b - 3 = 0$,解得 $a = 1$,$b = 3$. 由三角形三边关系可知 $3 - 1<c<3 + 1$,所以 $2<c<4$. 又因为 $c$ 为正整数,所以 $c = 3$,所以 $\triangle ABC$ 的周长为 $1+3+3 = 7$.
20[2024广东河源期末]综合与探究
【阅读理解】
图形是一种重要的数学语言,它直观形象,能有效地表示一些代数中数的关系,而运用代数思想也能巧妙地解决一些图形问题,“以数解形”“以形助数”就是数学中非常重要的思想方法——数形结合.
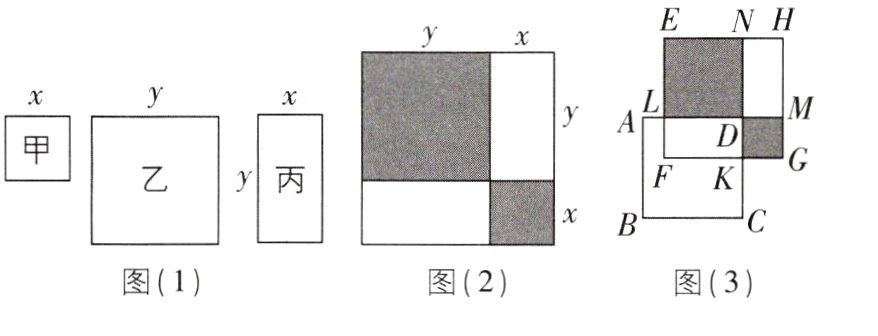
某数学学习小组在研究数形结合思想方法时,准备了若干张如图(1)所示的甲、乙、丙三种纸片,其中,甲种纸片是边长为 $x$ 的正方形,乙种纸片是边长为 $y$ 的正方形,丙种纸片是长为 $y$、宽为 $x$ 的长方形,并用甲种纸片一张、乙种纸片一张、丙种纸片两张拼成了如图(2)所示的一个大正方形.
(1)观察图(2),用两种不同的方式表示阴影部分的面积可得到等式________.
(2)利用(1)中的等式解决问题:若 $x + y = 10$,$xy = 19$,则 $x^{2}+y^{2}$ 的值为________.
【拓展探究】
该学习小组在研究过程中还发现一些较为复杂的式子能用下面方法求解.
例:若 $x$ 满足 $(20 - x)(x - 30)=10$,求 $(20 - x)^{2}+(x - 30)^{2}$ 的值.
解:设 $a = 20 - x$,$b = x - 30$,
则 $(20 - x)(x - 30)=ab = 10$,$a + b=(20 - x)+(x - 30)=20 - 30=-10$,
所以 $(20 - x)^{2}+(x - 30)^{2}=a^{2}+b^{2}=(a + b)^{2}-2ab=(-10)^{2}-2\times10 = 80$.
(3)如图(3),将正方形 $EFGH$ 叠放在正方形 $ABCD$ 上,重叠部分 $LFKD$ 是一个长方形,$AL = 2$,$CK = 6$. 沿着 $LD$,$KD$ 所在直线将正方形 $EFGH$ 分割成四个部分,若四边形 $ELDN$ 和四边形 $DKGM$ 恰好为正方形,且它们的面积之和为38,求长方形 $NDMH$ 的面积.
【阅读理解】
图形是一种重要的数学语言,它直观形象,能有效地表示一些代数中数的关系,而运用代数思想也能巧妙地解决一些图形问题,“以数解形”“以形助数”就是数学中非常重要的思想方法——数形结合.
某数学学习小组在研究数形结合思想方法时,准备了若干张如图(1)所示的甲、乙、丙三种纸片,其中,甲种纸片是边长为 $x$ 的正方形,乙种纸片是边长为 $y$ 的正方形,丙种纸片是长为 $y$、宽为 $x$ 的长方形,并用甲种纸片一张、乙种纸片一张、丙种纸片两张拼成了如图(2)所示的一个大正方形.
(1)观察图(2),用两种不同的方式表示阴影部分的面积可得到等式________.
(2)利用(1)中的等式解决问题:若 $x + y = 10$,$xy = 19$,则 $x^{2}+y^{2}$ 的值为________.
【拓展探究】
该学习小组在研究过程中还发现一些较为复杂的式子能用下面方法求解.
例:若 $x$ 满足 $(20 - x)(x - 30)=10$,求 $(20 - x)^{2}+(x - 30)^{2}$ 的值.
解:设 $a = 20 - x$,$b = x - 30$,
则 $(20 - x)(x - 30)=ab = 10$,$a + b=(20 - x)+(x - 30)=20 - 30=-10$,
所以 $(20 - x)^{2}+(x - 30)^{2}=a^{2}+b^{2}=(a + b)^{2}-2ab=(-10)^{2}-2\times10 = 80$.
(3)如图(3),将正方形 $EFGH$ 叠放在正方形 $ABCD$ 上,重叠部分 $LFKD$ 是一个长方形,$AL = 2$,$CK = 6$. 沿着 $LD$,$KD$ 所在直线将正方形 $EFGH$ 分割成四个部分,若四边形 $ELDN$ 和四边形 $DKGM$ 恰好为正方形,且它们的面积之和为38,求长方形 $NDMH$ 的面积.

答案:
【解】(1)第一种:因为阴影部分为一个边长为 $y$ 的正方形和一个边长为 $x$ 的正方形,所以 $S_{阴影部分}=x^{2}+y^{2}$.
查看更多完整答案,请扫码查看


