《2025年初中必刷题七年级数学下册苏科版》

1[2023江苏无锡期中]若(a² + b² + 1)(a² + b² - 1)= 35,则a² + b² = （ ）
A. 3　　　
　B. 6　　　
　C. ±3　　
　D. ±6

答案： B【解析】因为$(a^2 + b^2 + 1)(a^2 + b^2 - 1)=35$，所以$[(a^2 + b^2)+1][(a^2 + b^2)-1]=35$，所以$(a^2 + b^2)^2 - 1=35$，所以$(a^2 + b^2)^2=36$. 因为$a^2 + b^2\geq0$，所以$a^2 + b^2=6$，故选B.

2[2023福建厦门期中,中]若a = 2022⁰,b = 2023×2021 - 2022²,c = (-$\frac{2}{3}$)²⁰²²×($\frac{3}{2}$)²⁰²³,则下列a,b,c的大小关系正确的是　　(　　　)
A. b＜a＜c　
　B. a＜b＜c　
　C. a＜c＜b　
　D. c＜b＜a

答案： A【解析】因为$a = 2022^0=1$，$b=(2022 + 1)\times(2022 - 1)-2022^2=2022^2 - 1 - 2022^2=-1$，$c=(-\frac{2}{3}\times\frac{3}{2})^{2022}\times\frac{3}{2}=(-1)^{2022}\times\frac{3}{2}=\frac{3}{2}$，所以$b ＜ a ＜ c$，故选A.

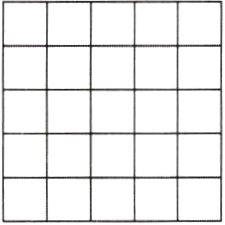
3[2024辽宁大连质检,中]如图,用大小相同的小正方形拼图形,第1个图形是一个小正方形；第2个图形由9个小正方形拼成；第3个图形由25个小正方形拼成,按此规律,若第n个图形比第(n - 1)个图形多用了72个小正方形,则n的值是________.

答案： 10【解析】因为第1个图形是一个小正方形；第2个图形由$9=(2\times2 - 1)^2$个小正方形拼成；第3个图形由$25=(2\times3 - 1)^2$个小正方形拼成，…，按此规律，拼成第$(n - 1)$个图形需要$(2n - 3)^2$个小正方形，拼成第$n$个图形需要$(2n - 1)^2$个小正方形，所以$(2n - 1)^2-(2n - 3)^2=72$，解得$n = 10$. 故答案为10.

4新考法[中]观察下列各式：
(a + 1)(a² - a + 1)= a³ + 1；
(a - 2)(a² + 2a + 4)= a³ - 8；
(3a - 2)(9a² + 6a + 4)= 27a³ - 8.
(1)请你按照以上各式的运算规律填空.
①(x - 3)(x² + 3x + 9)= ________；
②(2x + 1)(　　　　　)= 8x³ + 1；
③(________)(x² + xy + y²)= x³ - y³.
(2)应用规律计算：(a² - b²)(a² + ab + b²)(a² - ab + b²).

答案： 【解】
(1)①$(x - 3)(x^2 + 3x + 9)=x^3 - 27$；
②$(2x + 1)(4x^2 - 2x + 1)=8x^3 + 1$；
③$(x - y)(x^2 + xy + y^2)=x^3 - y^3$.
故答案为$x^3 - 27$，$4x^2 - 2x + 1$，$x - y$.
(2)$(a^2 - b^2)(a^2 + ab + b^2)(a^2 - ab + b^2)=[(a + b)(a^2 - ab + b^2)][(a - b)(a^2 + ab + b^2)]=(a^3 + b^3)(a^3 - b^3)=a^6 - b^6$.

5[2024江苏常州质检,中]乘法公式的探究与应用：
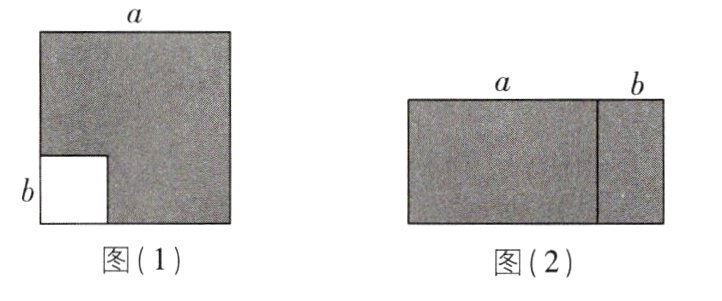
(1)如图(1),边长为a的大正方形中有一个边长为b的小正方形,则阴影部分的面积是________(写成两数平方差的形式).
(2)小颖将阴影部分裁下来,重新拼成一个大长方形,如图(2),则大长方形的长是________,宽是________,面积是________(写成多项式乘法的形式).
(3)比较图(1)、图(2)阴影部分的面积,可以得到恒等式：________________.
(4)运用你得到的公式计算：10.3×9.7.

答案： 【解】
(1)阴影部分的面积=大正方形的面积 - 小正方形的面积，即$a^2 - b^2$.
故答案为$a^2 - b^2$.
(2)大长方形的长是$a + b$，宽是$a - b$，面积是$(a + b)(a - b)$.
故答案为$a + b$，$a - b$，$(a + b)\cdot(a - b)$.
(3)$(a + b)(a - b)=a^2 - b^2$.
(4)$10.3\times9.7=(10 + 0.3)(10 - 0.3)=10^2 - 0.3^2=100 - 0.09=99.91$.

6核心素养推理能力[难]观察下列各式：
(a - b)(a + b)= a² - b²；(a - b)(a² + ab + b²)= a³ - b³；(a - b)(a³ + a²b + ab² + b³)= a⁴ - b⁴；(a - b)(a⁴ + a³b + a²b² + ab³ + b⁴)= a⁵ - b⁵……
(1)根据规律可得(a - b)(aⁿ⁻¹ + aⁿ⁻²b + aⁿ⁻³b² + … + a²bⁿ⁻³ + abⁿ⁻² + bⁿ⁻¹)= ________(其中n为正整数)；
(2)根据规律可得(a - 1)(aⁿ⁻¹ + aⁿ⁻² + … + a² + a + 1)= ________(其中n为正整数)；
(3)利用这个规律,请你解决下面的问题：
①求2¹⁹⁹ + 2¹⁹⁸ + 2¹⁹⁷ + … + 2² + 2 + 1的值；
②若a⁷ + a⁶ + a⁵ + a⁴ + a³ + a² + a + 1 = 0,求a的值.

答案：
(1)$a^n - b^n$
(2)$a^n - 1$
(3)【解】①因为$(2 - 1)(2^{199}+2^{198}+2^{197}+\cdots+2^2 + 2 + 1)=2^{200}-1$，所以$2^{199}+2^{198}+2^{197}+\cdots+2^2 + 2 + 1=2^{200}-1$.
②由
(2)可知，$a^8 - 1=(a - 1)(a^7 + a^6 + a^5 + a^4 + a^3 + a^2 + a + 1)$，
所以$a^8 - 1=0$，即$a^8 = 1$，
所以$a=\pm1$.
又因为当$a = 1$时，$a^7 + a^6 + a^5 + a^4 + a^3 + a^2 + a + 1=0$不成立，所以$a=-1$.
本题主要考查利用完全平方公式变形求图形面积，熟练运用完全平方公式是解题关键.
根据完全平方公式得到$(m - 1)x=\pm2\times3\times2x$是解答本题的关键