第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1[2024江苏无锡新吴区调研]下列是一元一次不等式组的是 ( )
A.$\begin{cases}x + 3 < 2,\\\frac{1}{x} + 2 \geq 5\end{cases}$
B.$\begin{cases}x + y > 4,\\x - y < 6\end{cases}$
C.$\begin{cases}x + 4 \geq -3,\\6 < 12\end{cases}$
D.$\begin{cases}x - 6 > -2,\\x + 1 < 8\end{cases}$
A.$\begin{cases}x + 3 < 2,\\\frac{1}{x} + 2 \geq 5\end{cases}$
B.$\begin{cases}x + y > 4,\\x - y < 6\end{cases}$
C.$\begin{cases}x + 4 \geq -3,\\6 < 12\end{cases}$
D.$\begin{cases}x - 6 > -2,\\x + 1 < 8\end{cases}$
答案:
刷基础
1. D 【解析】A 该不等式组中的第二个不等式的不等号左边不是整式,故本选项不合题意;B 该不等式组中有两个未知数,故本选项不合题意;C 该不等式组中的第二个不等式中不含有未知数,故本选项不合题意;D 该不等式组符合一元一次不等式组的定义,故本选项符合题意。
1. D 【解析】A 该不等式组中的第二个不等式的不等号左边不是整式,故本选项不合题意;B 该不等式组中有两个未知数,故本选项不合题意;C 该不等式组中的第二个不等式中不含有未知数,故本选项不合题意;D 该不等式组符合一元一次不等式组的定义,故本选项符合题意。
2[2024江苏苏州期中]不等式组$\begin{cases}x > 0,\\x < 1\end{cases}$的解集是 ( )
A.$x < 1$
B.$x > 0$
C.无解
D.$0 < x < 1$
A.$x < 1$
B.$x > 0$
C.无解
D.$0 < x < 1$
答案:
2. D 【解析】不等式组$\begin{cases}x>0 \\ x<1\end{cases}$的解集为$0<x<1$。刷有所得,故选 D。
3把不等式组$\begin{cases}x + 1 > 0,\\x + 3 \leq 4\end{cases}$的解集表示在数轴上,下列选项正确的是 ( )
−2−1012−2−1012
A B
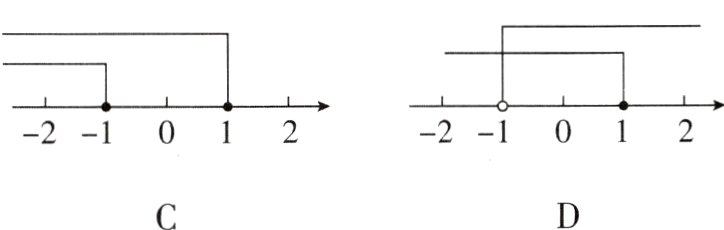
−2−1012−2−1012
A B
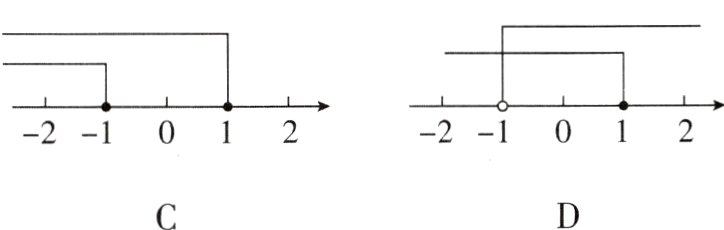
答案:
3. D 【解析】$\begin{cases}x + 1>0,① \\ x + 3\leq4,②\end{cases}$由①得$x>-1$,由②得$x\leq1$,所以不等式组的解集为$-1<x\leq1$,故选 D。
4[2024江苏徐州期末]某数学兴趣小组对关于x的不等式组$\begin{cases}x > 3,\\x \leq m\end{cases}$展开讨论并得到以下结论,其中正确的是 ( )
A.若$m = 5$,则不等式组的解集为$3 < x \leq 5$
B.若不等式组无解,则$m$的取值范围为$m < 3$
C.若$m = 2$,则不等式组的解集为$3 < x \leq 2$
D.若不等式组有解,则$m$的取值范围为$m \geq 3$
A.若$m = 5$,则不等式组的解集为$3 < x \leq 5$
B.若不等式组无解,则$m$的取值范围为$m < 3$
C.若$m = 2$,则不等式组的解集为$3 < x \leq 2$
D.若不等式组有解,则$m$的取值范围为$m \geq 3$
答案:
4. A 【解析】A 选项,当$m = 5$时,$\begin{cases}x>3 \\ x\leq5\end{cases}$,则不等式组的解集为$3<x\leq5$,故本选项正确,符合题意;B 选项,若不等式组无解,则$m$的取值范围为$m\leq3$,故本选项错误,不符合题意;C 选项,当$m = 2$时,$\begin{cases}x>3 \\ x\leq2\end{cases}$,则不等式组无解,故本选项错误,不符合题意;D 选项,若不等式组有解,则$m$的取值范围为$m>3$,故本选项错误,不符合题意。故选 A。
5新考向 开放性试题[2024浙江绍兴期末]写出解集是$-1 < x \leq 3$的一个不等式组:_______.
答案:
5. $\begin{cases}x\leq3 \\ x>-1\end{cases}$(答案不唯一)【解析】根据解集$-1<x\leq3$构造的不等式组可以为$\begin{cases}x\leq3 \\ x>-1\end{cases}$。故答案为$\begin{cases}x\leq3 \\ x>-1\end{cases}$(答案不唯一)
5. $\begin{cases}x\leq3 \\ x>-1\end{cases}$(答案不唯一)【解析】根据解集$-1<x\leq3$构造的不等式组可以为$\begin{cases}x\leq3 \\ x>-1\end{cases}$。故答案为$\begin{cases}x\leq3 \\ x>-1\end{cases}$(答案不唯一)

6[2024广东广州期末]不等式组$\begin{cases}x > 2,\\x > m + 1\end{cases}$的解集是$x > 2$,则$-2m + 4$的取值范围是_______.
答案:
6. $-2m + 4\geq2$【解析】因为不等式组$\begin{cases}x>2 \\ x>m + 1\end{cases}$的解集是$x>2$,所以$m + 1\leq2$,解得$m\leq1$,所以$-2m\geq - 2$,所以$-2m + 4\geq2$。故答案为$-2m + 4\geq2$。
7[2024江苏徐州质检]已知关于x的不等式组$\begin{cases}3x + m < 0,\\x > -5\end{cases}$的所有整数解的和为$-9$,求$m$的取值范围.
答案:
7. 【解】$\begin{cases}3x + m<0,① \\ x>-5,②\end{cases}$由①得$x<-\frac{m}{3}$。因为不等式组有解,所以不等式组的解集为$-5<x<-\frac{m}{3}$。因为不等式组的所有整数解的和为$-9$,所以不等式组的整数解为$-4,-3,-2$或$-4,-3,-2,-1,0,1$。当不等式组的整数解为$-4,-3,-2$时,有$-2<-\frac{m}{3}\leq - 1$,所以$m$的取值范围为$3\leq m<6$;当不等式组的整数解为$-4,-3,-2,-1,0,1$时,有$1<-\frac{m}{3}\leq2$,所以$m$的取值范围为$-6\leq m<-3$,所以$m$的取值范围是$-6\leq m<-3$或$3\leq m<6$。
不等式组解集的四种类型



思路分析:根据不等式组的解集即可列出关于$m$的不等式,求出$m$的取值范围,从而得出结论。
关键点拨:先求出每个不等式的解集,再求出不等式组的解集,根据不等式组整数解的个数即可得出答案。
7. 【解】$\begin{cases}3x + m<0,① \\ x>-5,②\end{cases}$由①得$x<-\frac{m}{3}$。因为不等式组有解,所以不等式组的解集为$-5<x<-\frac{m}{3}$。因为不等式组的所有整数解的和为$-9$,所以不等式组的整数解为$-4,-3,-2$或$-4,-3,-2,-1,0,1$。当不等式组的整数解为$-4,-3,-2$时,有$-2<-\frac{m}{3}\leq - 1$,所以$m$的取值范围为$3\leq m<6$;当不等式组的整数解为$-4,-3,-2,-1,0,1$时,有$1<-\frac{m}{3}\leq2$,所以$m$的取值范围为$-6\leq m<-3$,所以$m$的取值范围是$-6\leq m<-3$或$3\leq m<6$。
不等式组解集的四种类型




思路分析:根据不等式组的解集即可列出关于$m$的不等式,求出$m$的取值范围,从而得出结论。
关键点拨:先求出每个不等式的解集,再求出不等式组的解集,根据不等式组整数解的个数即可得出答案。
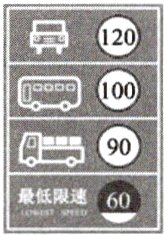
8[2024广东深圳期末]小明一家驾驶一辆小轿车外出旅游,经过某段高速公路时看到该段路对行驶车辆的限速规定如图所示,设小明家车辆经过该路段的速度为$v$千米/时,则符合限速规定的$v$应满足的条件是 ( )
A.$v \leq 120$
B.$v \leq 100$
C.$60 \leq v \leq 120$
D.$v \geq 60$

A.$v \leq 120$
B.$v \leq 100$
C.$60 \leq v \leq 120$
D.$v \geq 60$
答案:
8. C 【解析】由题图可知最低限速为$60$千米/时,小轿车的最高速度不超过$120$千米/时,所以$60\leq v\leq120$。故选 C。
9[2024江苏宿迁期末]列不等式组:$2x$与$3$的和不小于$4$,且$x$与$6$的差是负数:_______.
答案:
9. $\begin{cases}2x + 3\geq4 \\ x - 6<0\end{cases}$【解析】因为$2x$与$3$的和不小于$4$,所以$2x + 3\geq4$。因为$x$与$6$的差是负数,所以$x - 6<0$,所以所列不等式组为$\begin{cases}2x + 3\geq4 \\ x - 6<0\end{cases}$。故答案为$\begin{cases}2x + 3\geq4 \\ x - 6<0\end{cases}$
9. $\begin{cases}2x + 3\geq4 \\ x - 6<0\end{cases}$【解析】因为$2x$与$3$的和不小于$4$,所以$2x + 3\geq4$。因为$x$与$6$的差是负数,所以$x - 6<0$,所以所列不等式组为$\begin{cases}2x + 3\geq4 \\ x - 6<0\end{cases}$。故答案为$\begin{cases}2x + 3\geq4 \\ x - 6<0\end{cases}$

10[2024湖北武汉期末]某校为了培养学生阅读的习惯,准备把一些书分给学生阅读,若每人分$3$本,则多$10$本;若每人分$5$本,则最后一人分到了书但不到$3$本书. 问共有多少名学生?设共有$x$名学生,则可列不等式组为_______.
答案:
10. $\begin{cases}(3x + 10)-5(x - 1)>0 \\ (3x + 10)-5(x - 1)<3\end{cases}$【解析】根据题意列不等式组为$\begin{cases}(3x + 10)-5(x - 1)>0 \\ (3x + 10)-5(x - 1)<3\end{cases}$。故答案为$\begin{cases}(3x + 10)-5(x - 1)>0 \\ (3x + 10)-5(x - 1)<3\end{cases}$
查看更多完整答案,请扫码查看


