《2025年初中必刷题七年级数学下册苏科版》

1[2024江苏盐城质检，中]甲、乙两人分别从相距40km的A、B两地出发，相向而行，如果甲比乙早出发1h，那么乙出发2h后，两人相遇；如果他们同时出发，那么2.5h后，两人相距5km，则甲从A地到B地需要（ ）
A.$\frac{10}{3}$h　　　　　　　
　B.20h
C.10h或20h　　　
　D.$\frac{10}{3}$h或10h

答案： D 【解析】设甲、乙两人的速度分别为x km/h，y km/h. 分两种情况：若同时出发2.5 h后，两人相遇前相距5 km，依题意得$\begin{cases}x + 2x + 2y = 40\\x + y=\frac{40 - 5}{2.5}\end{cases}$，解得$\begin{cases}x = 12\\y = 2\end{cases}$；若同时出发2.5 h后，两人相遇后相距5 km，依题意得$\begin{cases}x + 2x + 2y = 40\\x + y=\frac{40 + 5}{2.5}\end{cases}$，解得$\begin{cases}x = 4\\y = 14\end{cases}$. 当甲的速度为12 km/h时，从A地到B地需要40÷12 = $\frac{10}{3}$(h)；当甲的速度为4 km/h时，从A地到B地需要40÷4 = 10(h). 故选D.

2[2024浙江湖州期末，中]同型号的甲、乙两辆测试车加满气体燃料后均可行驶120千米，即它们各自单独行驶并返回的最远距离是60千米. 如图，甲、乙两车加满气体燃料后都从A地出发，行驶途中停下来从甲车的气体燃料桶抽了一些气体燃料注入乙车的气体燃料桶，直至注满，然后甲车立即掉头返回A地，乙车继续行驶，到B地后立即掉头返回A地. 最终两车都到达A地，则B地最远可距离A地________千米.
　　　　　

答案：
80 【解析】如图，设甲车行驶到C地时返回，到达A地时燃料刚好用完，乙车行驶到B地后返回，到达A地时燃料用完，设AB = x km，AC = y km. 根据题意得$\begin{cases}2x + 2y = 120×2\\x - y + x = 120\end{cases}$，解得$\begin{cases}x = 80\\y = 40\end{cases}$，所以B地最远可距离A地80千米. 故答案为80.

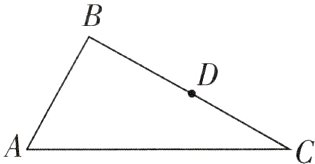
3[2024四川成都调研，中]如图，有一条三角形的环路，A至B段是上坡路，B至C段是下坡路，A至C段是平路，A至B，B至C，C至A三段距离的比是3:4:5，小琼和小芳同时从A出发，小琼按顺时针方向行走，小芳按逆时针方向行走，2.5小时后在BC上的D点相遇，已知两人上坡速度是4千米/时，下坡速度是6千米/时，在平路上的速度是5千米/时. 问C至D段是多少千米?
　　　　　　　　　　　

答案： 【解】设AB = 3a千米，BC = 4a千米，AC = 5a千米，CD = x千米.由题意得$\begin{cases}\frac{3a}{4}+\frac{4a - x}{6}=2.5\\\frac{5a}{5}+\frac{x}{4}=2.5\end{cases}$，解得x = a = 2.答：C至D段为2千米.

4[2024江苏宿迁宿豫区期末，中]一只小船从A 港口顺流航行到B港口需6h，而从B港口返回到A港口需8h. 某日，这只小船在上午6时出发，顺流航行到B港口时，发现船上一个救生圈在途中掉入水中，于是立即返回寻找救生圈，于1h后找到救生圈.
　(1)若小船按水流速度从A港口漂流到B港口需要多长时间？
　(2)救生圈何时掉入水中？

答案： 【解】
(1)设小船在静水中的速度为a，水流速度为b，A、B港口的距离为s.根据题意得$\begin{cases}s = 6(a + b)\\s = 8(a - b)\end{cases}$，解得$\begin{cases}a=\frac{7}{48}s\\b=\frac{1}{48}s\end{cases}$，所以小船按水流速度从A港口漂流到B港口的时间为$\frac{s}{b}=\frac{s}{\frac{s}{48}} = 48$(h).答：小船按水流速度从A港口漂流到B港口需要48 h.
(2)设A、B港口的距离为s，救生圈在出发t小时后掉入水中，则救生圈从掉入水中到被找到共在水中漂流了(6 - t + 1)h.根据题意得$\frac{1}{6}st+(6 - t + 1)\frac{1}{48}s+\frac{1}{8}s = s$，解得t = 5，而6 + 5 = 11，即救生圈在上午11时掉入水中.答：救生圈在上午11时掉入水中.

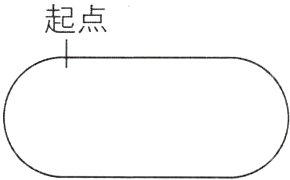
5[2024广东梅州一模，较难]周末，小明和他的爸爸到环形运动场进行跑步锻炼，如图，绕环形运动场一圈的路程为400m.
　(1)若两人同时同起点相向而跑，则经过36s后首次相遇；若两人同时同起点同向而跑，则经过180s后，爸爸首次从后面追上小明，问小明和他的爸爸的速度各为多少？
　(2)假设爸爸的速度是6m/s，小明的速度是5m/s，两人进行400m赛跑，同时同起点同向出发，等爸爸跑到半圈时，故意降速至4m/s，若爸爸按此速度继续比赛，小明能否在400m终点前追上爸爸？如果能，求追上时距离终点还有多少米；如果不能，请说明理由.
　　　　　　　　　　　　

答案： 【解】
(1)设小明的速度为x m/s，爸爸的速度为y m/s.依题意得$\begin{cases}36(x + y) = 400\\180(y - x) = 400\end{cases}$，解得$\begin{cases}x=\frac{40}{9}\\y=\frac{20}{3}\end{cases}$.答：小明的速度为$\frac{40}{9}$m/s，爸爸的速度为$\frac{20}{3}$m/s.
(2)小明能在400 m终点前追上爸爸，追上时距离终点还有$\frac{200}{3}$m.理由：爸爸跑到半圈所用时间为$\frac{200}{6}=\frac{100}{3}$(s)，此时小明所跑路程为$\frac{100}{3}×5=\frac{500}{3}$(m)，所以此时爸爸和小明的距离为200 - $\frac{500}{3}=\frac{100}{3}$(m)，所以小明接下来追上爸爸所需时间为$\frac{100}{3}$÷(5 - 4) = $\frac{100}{3}$(s)，追上时，爸爸共跑了200+$\frac{100}{3}×4=\frac{1000}{3}$(m)＜400 m，所以小明能在400 m终点前追上爸爸，追上时距离终点还有400 - $\frac{1000}{3}=\frac{200}{3}$(m).