《2025年初中必刷题七年级数学下册苏科版》

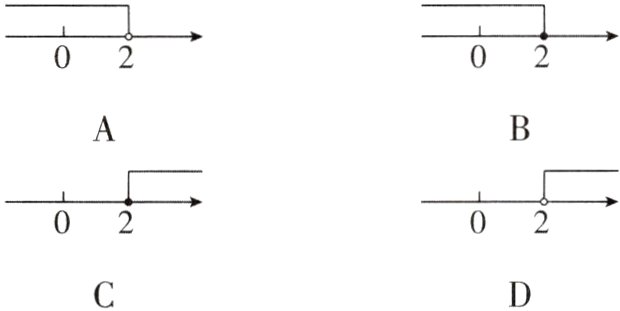
1[2024吉林长春期末]不等式3x - 1 ≤ x + 3的解集在数轴上表示正确的是（ ）

A.
B.
C.
D.

答案： B【解析】$3x - 1 \leq x + 3$，移项、合并同类项，得$2x \leq 4$，解得$x \leq 2$。在数轴上表示为$\begin{matrix} \text{———} \\ 0 \quad 2 \end{matrix}$。故选B。

2[2024江苏泰州期末]已知|2x - 5| = 5 - 2x，则x的取值范围是（ ）
A. x ＜ $\frac{2}{5}$
B. x ≤ $\frac{2}{5}$
C. x ＜ $\frac{5}{2}$
D. x ≤ $\frac{5}{2}$

答案： D【解析】因为$|2x - 5| = 5 - 2x$，所以$2x - 5 \leq 0$，解得$x \leq \frac{5}{2}$。故选D。

3[2024安徽合肥期中]要使代数式4x - 7的值不小于代数式8x + 5的值，x可以是（ ）
A. -2
B. 4
C. -4
D. 2

答案： C【解析】根据题意，得$4x - 7 \geq 8x + 5$。移项得$4x - 8x \geq 5 + 7$。合并同类项，得$-4x \geq 12$。解得$x \leq -3$，只有 -4 符合。故选C。

4[2023北京海淀区质检]已知关于x的不等式x - a ≤ -2的解集表示在数轴上如图所示，那么a的值是________.

答案： 1【解析】因为$x - a \leq -2$，所以$x \leq a - 2$。又由题图可知不等式$x - a \leq -2$的解集为$x \leq -1$，所以$a - 2 = -1$，所以$a = 1$。故答案为1。

5[2023江苏淮安期末]若关于x的方程x + k = 2x - 1的解是负数，则k的取值范围是________.

答案： $k ＜ -1$【解析】$x + k = 2x - 1$，整理得$x = k + 1$。因为关于$x$的方程$x + k = 2x - 1$的解是负数，所以$k + 1 ＜ 0$，解得$k ＜ -1$。故答案为$k ＜ -1$。

6[2023江苏泰州调研]解下列不等式，并把它们的解集在数轴上表示出来.
（1）2x - 1 ＜ 3x + 2；
（2）2(x + 3) - 4x ＜ -(x - 1).

答案： 【解】
(1)移项，得$2x - 3x ＜ 2 + 1$。合并同类项，得$-x ＜ 3$。不等式的两边都除以 -1，得$x ＞ -3$。将这个不等式的解集在数轴上表示如下：$\begin{matrix} \text{————} \\ -4 \ -3 \ -2 \ -1 \ 0 \ 1 \ 2 \end{matrix}$
(2)去括号，得$2x + 6 - 4x ＜ -x + 1$。移项，得$2x - 4x + x ＜ 1 - 6$。合并同类项，得$-x ＜ -5$。不等式的两边都除以 -1，得$x ＞ 5$。将这个不等式的解集在数轴上表示如下：$\begin{matrix} \text{————} \\ 0 \ 1 \ 2 \ 3 \ 4 \ 5 \ 6 \ 7 \ 8 \end{matrix}$
易错警示
负数的绝对值是其相反数；0的绝对值是0，也是其相反数，所以本题中$2x - 5 \leq 0$，注意不要漏掉等于0的情况。
易错警示
本题运用不等式的基本性质2去分母，不等式的所有项必须同时乘6，才能保证不等式依然成立，注意不要漏乘没有分母的项。

7[2024江苏盐城质检]若方程组$\begin{cases}3x + y = k + 1,\\x + 3y = 3\end{cases}$的解为$\begin{cases}x = a,\\y = b,\end{cases}$且a + b ＞ 0，则k的取值范围是（ ）
A. k ＞ 4
B. k ＞ -4
C. k ＜ 4
D. k ＜ -4

答案： B【解析】将$\begin{cases} x = a \\ y = b \end{cases}$代入原方程组得$\begin{cases} 3a + b = k + 1, &① \\ a + 3b = 3, &② \end{cases}$，$\frac{① + ②}{4}$，得$a + b = \frac{k + 4}{4}$。因为$a + b ＞ 0$，所以$\frac{k + 4}{4} ＞ 0$，解得$k ＞ -4$。故选B。

8不等式 - x - 5 + $\frac{x - 1}{3}$ ≤ $\frac{2x + 3}{2}$的最小整数解是________.

答案： -4【解析】解不等式$-x - 5 + \frac{x - 1}{3} \leq \frac{2x + 3}{2}$，得$x \geq -4.1$，所以该不等式的最小整数解是 -4。

9[2023江苏盐城调研]若方程组$\begin{cases}x + 2y = 1 + m,\\2x + y = -3\end{cases}$中的x，y满足x + y ＞ 0，则m的取值范围是________.

答案： $m ＞ 2$【解析】$\begin{cases} x + 2y = 1 + m \\ 2x + y = -3 \end{cases}$，两式相加，得$3x + 3y = m - 2$，则$x + y = \frac{m - 2}{3}$。因为$x + y ＞ 0$，所以$\frac{m - 2}{3} ＞ 0$，解得$m ＞ 2$，故答案为$m ＞ 2$。

10[2023江苏扬州期末]解下列不等式，并把它们的解集在数轴上表示出来.
（1）1 - $\frac{x + 6}{2}$ ≤ $\frac{2x + 1}{3}$；
（2）$\frac{2x}{3} - \frac{6x + 1}{6}$ ≤ 1.

答案：
【解】
(1)去分母，得$6 - 3(x + 6) \leq 2(2x + 1)$。去括号，得$6 - 3x - 18 \leq 4x + 2$。移项，得$-3x - 4x \leq 2 - 6 + 18$。合并同类项，得$-7x \leq 14$。两边都除以 -7，得$x \geq -2$。这个不等式的解集在数轴上表示如下：

(2)去分母，得$4x - (6x + 1) \leq 6$。去括号，得$4x - 6x - 1 \leq 6$。移项，得$4x - 6x \leq 6 + 1$。合并同类项，得$-2x \leq 7$。两边都除以 -2，得$x \geq - \frac{7}{2}$。其解集在数轴上表示如下：$\begin{matrix} \text{————} \\ -5 \ -4 \ -3 \ -2 \ -1 \ 0 \ 1 \ 2 \ 3 \ 4 \ 5 \end{matrix}$

11[2024浙江湖州期末]解不等式$\frac{1 + x}{2}$ ≤ $\frac{1 + 2x}{3}$ + 1时，去分母正确的是（ ）
A. 1 + x ≤ 1 + 2x + 1
B. 1 + x ≤ 1 + 2x + 6
C. 3(1 + x) ≤ 2(1 + 2x) + 1
D. 3(1 + x) ≤ 2(1 + 2x) + 6

答案： D【解析】不等式两边都乘6，得$3(1 + x) \leq 2(1 + 2x) + 6$。故选D。

1[2024四川自贡质检，中]若数3是关于x的不等式2x - a - 2 ＜ 0的一个解，则a可取的最小正整数为（ ）
A. 3
B. 4
C. 5
D. 6

答案： C【解析】由不等式$2x - a - 2 ＜ 0$，得$x ＜ \frac{a + 2}{2}$。
∵数3是不等式$2x - a - 2 ＜ 0$的一个解，$\therefore \frac{a + 2}{2} ＞ 3$，$\therefore a ＞ 4$，$\therefore a$可取的最小正整数为5，故选C。