第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1. [中]已知A地在B地的正西方向,且有一以A,B两地为端点的东西向直线道路,其全长为400千米. 今在此道路上距离A地12千米处设置第一个广告牌,之后每往东27千米就设置一个广告牌,如图所示. 若某车从此道路上距离A地19千米处出发,往东直行320千米后才停止,则此车在停止前经过的最后一个广告牌距离A地________千米.


答案:
336 【解析】设此车停止时在车的正西方向有x个广告牌. 根据题意,得$12 + 27(x - 1)\leq320 + 19$,解得$x\leq13\frac{1}{9}$,即此车停止时在车的正西方向有13个广告牌,并且超过第13个广告牌3千米,所以此车在停止前经过的最后一个广告牌距离A地$320 + 19 - 3 = 336$(千米),故答案为336.
2. [2024江苏无锡质检,较难]某小区内有甲、乙两种儿童电动汽车,租用一次甲种电动汽车前15分钟内(包括15分钟)收费15元,超过15分钟后每超过1分钟加收1元(不足1分钟都按1分钟收费);乙种电动汽车前10分钟内(包括10分钟)收费5元,超过10分钟后每超过2分钟加收3元(不足2分钟都按2分钟收费).
(1)小明租用的是乙种电动汽车,用时15分钟需缴费________元;
(2)如果小明租用了其中一种电动汽车,用时x分钟,那么当x满足________时,租用甲种电动汽车比乙种电动汽车费用少.
(1)小明租用的是乙种电动汽车,用时15分钟需缴费________元;
(2)如果小明租用了其中一种电动汽车,用时x分钟,那么当x满足________时,租用甲种电动汽车比乙种电动汽车费用少.
答案:
(1)14
(2)$18<x\leq19$或$x>20$
【解析】
(1)小明租用乙种电动汽车用时15分钟需缴费$5 + 3\times3 = 14$(元).
(2)当$0<x\leq10$时,租用甲种电动汽车需缴费15元,租用乙种电动汽车需缴费5元,不符合题意;当$10<x\leq15$时,租用甲种电动汽车需缴费15元,由
(1)可知租用乙种电动汽车最多需缴费$5 + 3\times3 = 14$(元),不符合题意;当$x>15$时,$15+(x - 15)\times1<5+\frac{x - 10}{2}\times3$,解得$x>20$.
因为甲种电动汽车不足1分钟都按1分钟收费,乙种电动汽车不足2分钟都按2分钟收费,所以当$19<x\leq20$时,租用甲种电动汽车需缴费$15+(20 - 15)\times1 = 20$(元),租用乙种电动汽车需缴费$5+\frac{20 - 10}{2}\times3 = 20$(元),此时费用相等;当$18<x\leq19$时,租用乙种电动汽车仍为20元,而甲种电动汽车需要19元,符合题意;当$15<x\leq16$,$16<x\leq17$,$17<x\leq18$时,同理可得租用甲种电动汽车的费用大于或等于租用乙种电动汽车的费用,不符合题意. 综上所述,x应满足$18<x\leq19$或$x>20$. 故答案为$18<x\leq19$或$x>20$.
(1)14
(2)$18<x\leq19$或$x>20$
【解析】
(1)小明租用乙种电动汽车用时15分钟需缴费$5 + 3\times3 = 14$(元).
(2)当$0<x\leq10$时,租用甲种电动汽车需缴费15元,租用乙种电动汽车需缴费5元,不符合题意;当$10<x\leq15$时,租用甲种电动汽车需缴费15元,由
(1)可知租用乙种电动汽车最多需缴费$5 + 3\times3 = 14$(元),不符合题意;当$x>15$时,$15+(x - 15)\times1<5+\frac{x - 10}{2}\times3$,解得$x>20$.
因为甲种电动汽车不足1分钟都按1分钟收费,乙种电动汽车不足2分钟都按2分钟收费,所以当$19<x\leq20$时,租用甲种电动汽车需缴费$15+(20 - 15)\times1 = 20$(元),租用乙种电动汽车需缴费$5+\frac{20 - 10}{2}\times3 = 20$(元),此时费用相等;当$18<x\leq19$时,租用乙种电动汽车仍为20元,而甲种电动汽车需要19元,符合题意;当$15<x\leq16$,$16<x\leq17$,$17<x\leq18$时,同理可得租用甲种电动汽车的费用大于或等于租用乙种电动汽车的费用,不符合题意. 综上所述,x应满足$18<x\leq19$或$x>20$. 故答案为$18<x\leq19$或$x>20$.
3. [2024广东广州期中,中]在车站开始检票时,有a(a>0)名旅客在候车室排队等候检票,检票开始后,仍有旅客前来进站,进站人数按固定速度(c人/分)增加,所有的检票口检票的速度为b人/分. 若车站只开放1个检票口,则需要30分钟才能把排队等候检票的旅客全部检票完毕;若只开放2个检票口,则需要10分钟才能把排队等候检票的旅客全部检票完毕.
(1)求a与b之间的数量关系.
(2)若要在5分钟内将排队等候检票的旅客全部检票完毕,减少旅客等待的时间,需要至少同时开放多少个检票口?
(1)求a与b之间的数量关系.
(2)若要在5分钟内将排队等候检票的旅客全部检票完毕,减少旅客等待的时间,需要至少同时开放多少个检票口?
答案:
【解】
(1)根据题意,得$\begin{cases}a + 30c = 30b&①\\a + 10c = 2\times10b&②\end{cases}$
由②×3 - ①,得$2a = 30b$,所以$a = 15b$.
(2)设5分钟内将排队等候检票的旅客全部检票完毕需要同时开放n个检票口.
根据题意,得$\begin{cases}a + 30c = 30b&①\\a + 10c = 2\times10b&②\\a + 5c\leq nb&③\end{cases}$
由②×3 - ①,得$2a = 30b$,所以$b=\frac{a}{15}$,④
把④代入①,得$c=\frac{a}{30}$,⑤
把④⑤代入③,得$a+\frac{a}{6}\leq n\times\frac{a}{3}$.
因为$a>0$,所以$n\geq\frac{7}{2}=3.5$.
答:需要至少同时开放4个检票口.
(1)根据题意,得$\begin{cases}a + 30c = 30b&①\\a + 10c = 2\times10b&②\end{cases}$
由②×3 - ①,得$2a = 30b$,所以$a = 15b$.
(2)设5分钟内将排队等候检票的旅客全部检票完毕需要同时开放n个检票口.
根据题意,得$\begin{cases}a + 30c = 30b&①\\a + 10c = 2\times10b&②\\a + 5c\leq nb&③\end{cases}$
由②×3 - ①,得$2a = 30b$,所以$b=\frac{a}{15}$,④
把④代入①,得$c=\frac{a}{30}$,⑤
把④⑤代入③,得$a+\frac{a}{6}\leq n\times\frac{a}{3}$.
因为$a>0$,所以$n\geq\frac{7}{2}=3.5$.
答:需要至少同时开放4个检票口.
4. [2024重庆沙坪坝区期末,中]如图,在△ABC中,AD是BC边上的高,BD = 8,DC = 6,AC = 10,点E在高AD上,且ED = 4,点P从点B出发,沿折线B→C→A方向以每秒2个单位长度的速度运动,到达点A时停止,设点P的运动时间为x秒.
(1)求点P整个运动过程共需多少秒.
(2)当点P在BC边上运动,且以点P,D,E为顶点的三角形是等腰直角三角形时,求x的值.
(3)当CP的长大于点P运动路程的$\frac{1}{4}$时,求x的取值范围.
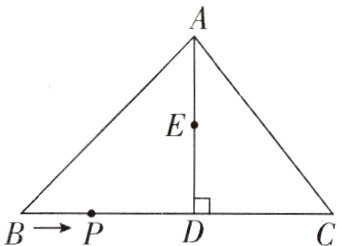
(1)求点P整个运动过程共需多少秒.
(2)当点P在BC边上运动,且以点P,D,E为顶点的三角形是等腰直角三角形时,求x的值.
(3)当CP的长大于点P运动路程的$\frac{1}{4}$时,求x的取值范围.

答案:
【解】
(1)$BD + CD + AC = 8 + 6 + 10 = 24$,$24\div2 = 12$(秒),即点P整个运动过程共需12秒.
(2)因为AD是BC边上的高,所以当点P在BC边上运动,且以点P,D,E为顶点的三角形是等腰直角三角形时,$DP = DE$. 当点P在点D左侧时,$DP = BD - BP = DE$,即$8 - 2x = 4$,解得$x = 2$;
当点P在点D右侧时,$DP = BP - BD = DE$,即$2x - 8 = 4$,解得$x = 6$.
综上可知,x的值为2或6.
(3)点P运动路程为2x,当点P在BC边上运动时,$CP = BC - BP = 8 + 6 - 2x = 14 - 2x$,令$14 - 2x>\frac{1}{4}\times2x$,解得$x<\frac{28}{5}$,所以$0\leq x<\frac{28}{5}$;
当点P在AC边上运动时,$CP = 2x - BC = 2x - 14$,则$2x - 14>\frac{1}{4}\times2x$,解得$x>\frac{28}{3}$.
因为点P整个运动过程共需12秒,所以$\frac{28}{3}<x\leq12$.
综上可知,x的取值范围为$0\leq x<\frac{28}{5}$或$\frac{28}{3}<x\leq12$.
关键点拔:分点P在BC边上运动时和点P在AC边上运动时两种情况,分别列出不等式求解即可.
(1)$BD + CD + AC = 8 + 6 + 10 = 24$,$24\div2 = 12$(秒),即点P整个运动过程共需12秒.
(2)因为AD是BC边上的高,所以当点P在BC边上运动,且以点P,D,E为顶点的三角形是等腰直角三角形时,$DP = DE$. 当点P在点D左侧时,$DP = BD - BP = DE$,即$8 - 2x = 4$,解得$x = 2$;
当点P在点D右侧时,$DP = BP - BD = DE$,即$2x - 8 = 4$,解得$x = 6$.
综上可知,x的值为2或6.
(3)点P运动路程为2x,当点P在BC边上运动时,$CP = BC - BP = 8 + 6 - 2x = 14 - 2x$,令$14 - 2x>\frac{1}{4}\times2x$,解得$x<\frac{28}{5}$,所以$0\leq x<\frac{28}{5}$;
当点P在AC边上运动时,$CP = 2x - BC = 2x - 14$,则$2x - 14>\frac{1}{4}\times2x$,解得$x>\frac{28}{3}$.
因为点P整个运动过程共需12秒,所以$\frac{28}{3}<x\leq12$.
综上可知,x的取值范围为$0\leq x<\frac{28}{5}$或$\frac{28}{3}<x\leq12$.
关键点拔:分点P在BC边上运动时和点P在AC边上运动时两种情况,分别列出不等式求解即可.
5. [较难]某公司有A、B两种型号的客车共20辆,它们的载客量、每天的租金如表所示. 已知在20辆客车都坐满的情况下,共载客720人.

(1)A、B两种型号的客车各有多少辆?
(2)某中学计划租用A、B两种型号的客车共8辆,送七年级师生到某教育基地参加社会实践活动,已知该中学租车的总费用不超过4600元,则最多能租用多少辆A型号客车?
(3)在(2)的条件下,若七年级的师生共有295人,请写出所有可能的租车方案,并确定最省钱的租车方案.

(1)A、B两种型号的客车各有多少辆?
(2)某中学计划租用A、B两种型号的客车共8辆,送七年级师生到某教育基地参加社会实践活动,已知该中学租车的总费用不超过4600元,则最多能租用多少辆A型号客车?
(3)在(2)的条件下,若七年级的师生共有295人,请写出所有可能的租车方案,并确定最省钱的租车方案.
答案:
【解】
(1)设A型号的客车有x辆,B型号的客车有y辆.
依题意得$\begin{cases}x + y = 20\\45x + 30y = 720\end{cases}$,解得$\begin{cases}x = 8\\y = 12\end{cases}$.
答:A型号的客车有8辆,B型号的客车有12辆.
(2)设租用m辆A型号客车,则租用$(8 - m)$辆B型号客车.
依题意得$600m + 450(8 - m)\leq4600$,解得$m\leq\frac{20}{3}$.
又因为m为整数,所以m的最大值为6.
答:最多能租用6辆A型号客车.
(3)依题意得$45m + 30(8 - m)\geq295$,解得$m\geq\frac{11}{3}$.
又因为m为整数,所以m的最小值为4.
结合
(2)可知m的值可以为4,5,6,所以共有3种租车方案,方案1:租用4辆A型号客车,4辆B型号客车;方案2:租用5辆A型号客车,3辆B型号客车;方案3:租用6辆A型号客车,2辆B型号客车.
选择租车方案1所需总费用为$600\times4 + 450\times4 = 4200$(元);
选择租车方案2所需总费用为$600\times5 + 450\times3 = 4350$(元);
选择租车方案3所需总费用为$600\times6 + 450\times2 = 4500$(元).
因为$4200<4350<4500$,所以最省钱的租车方案为租用4辆A型号客车,4辆B型号客车.
关键点拔:根据租用的8辆客车可乘坐人数不少于295,可得出关于m的一元一次不等式,再结合
(2)中的结论,且m为整数即可求解.
(1)设A型号的客车有x辆,B型号的客车有y辆.
依题意得$\begin{cases}x + y = 20\\45x + 30y = 720\end{cases}$,解得$\begin{cases}x = 8\\y = 12\end{cases}$.
答:A型号的客车有8辆,B型号的客车有12辆.
(2)设租用m辆A型号客车,则租用$(8 - m)$辆B型号客车.
依题意得$600m + 450(8 - m)\leq4600$,解得$m\leq\frac{20}{3}$.
又因为m为整数,所以m的最大值为6.
答:最多能租用6辆A型号客车.
(3)依题意得$45m + 30(8 - m)\geq295$,解得$m\geq\frac{11}{3}$.
又因为m为整数,所以m的最小值为4.
结合
(2)可知m的值可以为4,5,6,所以共有3种租车方案,方案1:租用4辆A型号客车,4辆B型号客车;方案2:租用5辆A型号客车,3辆B型号客车;方案3:租用6辆A型号客车,2辆B型号客车.
选择租车方案1所需总费用为$600\times4 + 450\times4 = 4200$(元);
选择租车方案2所需总费用为$600\times5 + 450\times3 = 4350$(元);
选择租车方案3所需总费用为$600\times6 + 450\times2 = 4500$(元).
因为$4200<4350<4500$,所以最省钱的租车方案为租用4辆A型号客车,4辆B型号客车.
关键点拔:根据租用的8辆客车可乘坐人数不少于295,可得出关于m的一元一次不等式,再结合
(2)中的结论,且m为整数即可求解.
查看更多完整答案,请扫码查看


