《2025年初中必刷题七年级数学下册苏科版》

1[2024江苏常州质检]下列四幅图案中，能由其中的一部分平移得到的是 （ ）

A B C D

答案： B【解析】四幅图案中，只有选项B中的图案能由其中的一部分平移得到。故选B。

2[2024浙江绍兴期末]下列物体的运动属于平移的是 （ ）
A. 汽车方向盘的转动
B. 小红荡秋千
C. 电梯的升降
D. 火车在弯曲的铁轨上行驶

答案： C【解析】A选项，汽车方向盘的转动，不是平移，不符合题意；B选项，小红荡秋千，不是平移，不符合题意；C选项，电梯的升降，是平移，符合题意；D选项，火车在弯曲的铁轨上行驶，不是平移，不符合题意。故选C。

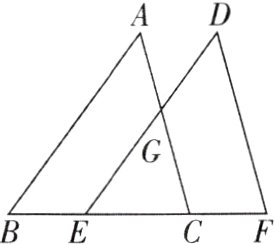
3[2023江苏南京建邺区期中]如图，三角形ABC沿着直线BC向右平移得到三角形DEF，则 ①BE = CF；②AB//DE；③AG = DG；④∠ACB = ∠DFE，其中结论正确的是 （ ）

A. ①②
B. ①②④
C. ②④
D. ①③④

答案： B【解析】因为三角形DEF是由三角形ABC沿着直线BC向右平移得到的，所以BC = EF，AC//DF，AB//DE，所以∠ACE = ∠DFE，BC - CE = EF - CE，所以BE = FC，故①②④正确。由平移的性质无法得到AG = DG，故③错误。故选B。

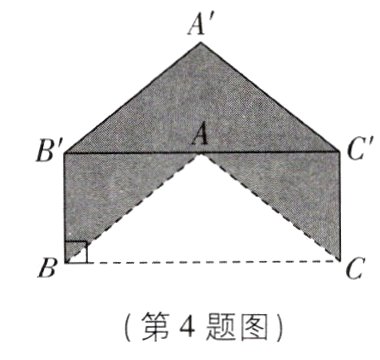
4[2024江苏南通期末]如图，△ABC的边BC的长为5 cm. 将△ABC向上平移2 cm得到△A'B'C'，点A在B'C'上，连接BB'，CC'，BB'⊥BC，则阴影部分的面积为 （ ）

A. 50 cm²
B. 25 cm²
C. 20 cm²
D. 10 cm²

答案： D【解析】由平移可知$S_{\triangle ABC}=S_{\triangle A'B'C'}$。由平移的性质可知四边形$BCC'B'$是长方形。又因为$BB' = 2\ cm$，$BC = 5\ cm$，所以$S_{阴影}=S_{\triangle A'B'C'}+S_{长方形BB'C'C}-S_{\triangle ABC}=S_{长方形BB'C'C}=BC\times BB' = 5\times2 = 10(cm^{2})$。故选D。
关键点拨
（2）仿照例题的思路，配成两个完全平方式，然后利用偶次方的非负性进行计算，即可解答；
（3）仿照例题的思路，配成两个完全平方式，再利用偶次方的非负性，先求出a，b的值，然后根据三角形的三边关系即可解答。
在平面内，将一个图形沿直线的某个方向平行移动一定的距离后得到另一个图形的平面变换叫作平移，新图形与原图形的形状和大小完全相同。
第二种：因为阴影部分的面积等于大正方形的面积减去两个长方形的面积，所以$S_{阴影部分}=(x + y)^{2}-2xy$，故$x^{2}+y^{2}=(x + y)^{2}-2xy$。故答案为$x^{2}+y^{2}=(x + y)^{2}-2xy$。
（2）因为$x + y = 10$，$xy = 19$，所以$x^{2}+y^{2}=(x + y)^{2}-2xy = 10^{2}-2\times19 = 62$。故答案为62。
（3）设$LD = x$，$DK = y$。因为四边形ELDN和四边形DKGM为正方形，所以$DN = LD = x$，$DM = DK = y$。因为四边形ABCD为正方形，所以$AD = CD$。因为$AD = AL + LD$，$CD = CK + DK$，所以$AL + LD = CK + DK$。因为$AL = 2$，$CK = 6$，所以$2 + x = 6 + y$，所以$x - y = 4$，所以$(x - y)^{2}=16$，所以$x^{2}-2xy + y^{2}=16$。因为正方形ELDN和正方形DKGM的面积之和为38，所以$x^{2}+y^{2}=38$，所以$38 - 2xy = 16$，所以$xy = 11$，所以$S_{长方形NDMH}=DN\cdot DM = DL\cdot DK = xy = 11$。

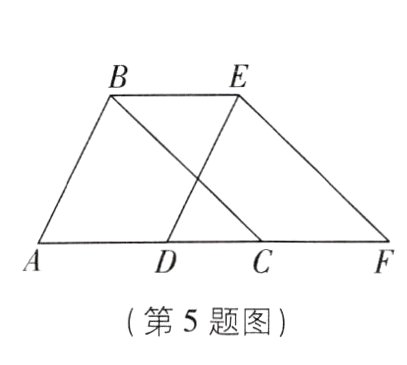
5[2024江苏无锡期末]如图，把△ABC沿着射线AC的方向平移得到△DEF，BE = 2，DC = 1.5，则AF = ________.

答案： 5.5【解析】由平移的性质可得$AD = CF = BE = 2$。因为$DC = 1.5$，所以$AF = AD + CD + CF = 5.5$。故答案为5.5。

6[2023江苏扬州广陵区期中]如图，将三角形ABC沿射线AB的方向平移2个单位得到三角形DEF，点A，B，C的对应点分别为点D，E，F.
(1)若AB = 3，则AE = ________.
(2)若∠ABC = 75°，求∠CFE的度数.

答案： 【解】
(1)因为$AB = 3$，将三角形ABC沿射线AB的方向平移2个单位得到三角形DEF，所以$BE = 2$，则$AE = BE + AB = 5$。故答案为5。
(2)由平移的性质得$BC//EF$，$AE//CF$，所以$\angle E=\angle ABC = 75^{\circ}$，$\angle CFE+\angle E = 180^{\circ}$，所以$\angle CFE = 105^{\circ}$。

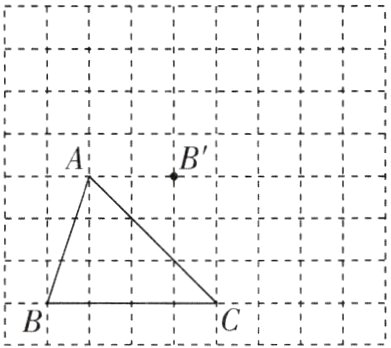
7[2024福建泉州期末]在如图所示的网格图中，每个小正方形的顶点称为“格点”，△ABC的三个顶点均在“格点”上，每个小正方形的边长均为1.
(1)在网格图中，将△ABC沿着射线BB'的方向平移，使点B与点B'对应，请画出平移得到的△A'B'C'；
(2)请直接写出直线BB'与线段A'C'的位置关系，不必说明理由；
(3)试求出在平移过程中，线段BC所扫过部分的面积.

答案：
【解】
(1)如图，$\triangle A'B'C'$即为所求。

(2)$BB'\perp A'C'$。理由：由网格图的特点可知$BB'\perp AC$。由平移知$AC//A'C'$，所以$BB'\perp A'C'$。
(3)如图，线段BC所扫过部分的面积为四边形$BCC'B'$的面积，即$4\times3 = 12$。