第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1[2023黑龙江齐齐哈尔中考]下列计算正确的是( )
A. $3b^{2}+b^{2}=4b^{4}$
B. $(a^{4})^{2}=a^{6}$
C. $(-x^{2})^{2}=x^{4}$
D. $3a\cdot2a = 6a$
A. $3b^{2}+b^{2}=4b^{4}$
B. $(a^{4})^{2}=a^{6}$
C. $(-x^{2})^{2}=x^{4}$
D. $3a\cdot2a = 6a$
答案:
C 【解析】$3b^{2}+b^{2}=4b^{2}$,则 A 选项不符合题意;$(a^{4})^{2}=a^{8}$,则 B 选项不符合题意;$(-x^{2})^{2}=x^{4}$,则 C 选项符合题意;$3a\cdot2a = 6a^{2}$,则 D 选项不符合题意. 故选 C.
2[2024湖北中考]计算 $2x\cdot3x^{2}$ 的结果是( )
A. $5x^{2}$
B. $6x^{2}$
C. $5x^{3}$
D. $6x^{3}$
A. $5x^{2}$
B. $6x^{2}$
C. $5x^{3}$
D. $6x^{3}$
答案:
D 【解析】$2x\cdot3x^{2}=6x^{3}$. 故选 D.
3[2024甘肃兰州中考]计算:$2a(a - 1)-2a^{2}=$( )
A. $a$
B. $-a$
C. $2a$
D. $-2a$
A. $a$
B. $-a$
C. $2a$
D. $-2a$
答案:
D 【解析】$2a(a - 1)-2a^{2}=2a^{2}-2a-2a^{2}=-2a$. 故选 D.
4[2023江苏常州中考]若圆柱的底面半径和高均为 $a$,则它的体积是________(用含 $a$ 的代数式表示).
答案:
$\pi a^{3}$ 【解析】根据圆柱的体积 = 圆柱的底面积×圆柱的高,可得圆柱的体积为 $\pi a^{2}\cdot a=\pi a^{3}$. 故答案为 $\pi a^{3}$.
5[2023吉林中考]计算:$a(b + 3)=$________.
答案:
$ab + 3a$ 【解析】$a(b + 3)=ab + 3a$. 故答案为 $ab + 3a$.
6[2023四川攀枝花中考]我们可以利用图形中的面积关系来解释很多代数恒等式. 给出以下4组图形及相应的代数恒等式:
①$(a + b)^{2}=a^{2}+2ab + b^{2}$ ②$(a - b)^{2}=a^{2}-2ab + b^{2}$
③$(a + b)(a - b)=a^{2}-b^{2}$ ④$(a - b)^{2}=(a + b)^{2}-4ab$

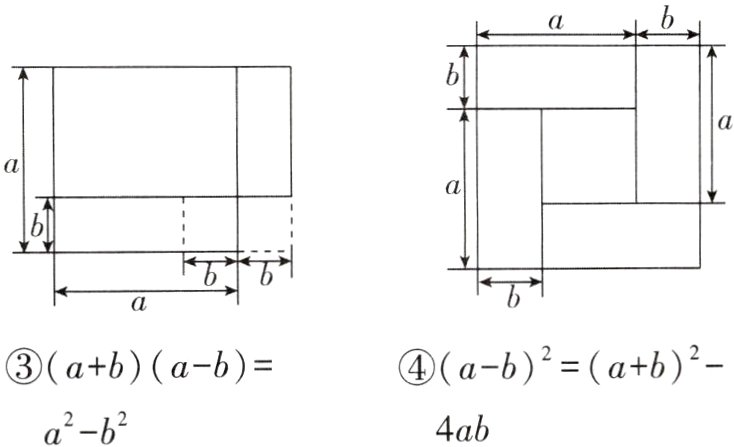
其中,图形的面积关系能正确解释相应的代数恒等式的有( )
A. 1个
B. 2个
C. 3个
D. 4个
①$(a + b)^{2}=a^{2}+2ab + b^{2}$ ②$(a - b)^{2}=a^{2}-2ab + b^{2}$
③$(a + b)(a - b)=a^{2}-b^{2}$ ④$(a - b)^{2}=(a + b)^{2}-4ab$


其中,图形的面积关系能正确解释相应的代数恒等式的有( )
A. 1个
B. 2个
C. 3个
D. 4个
答案:
D 【解析】图形的面积关系能正确解释相应的代数恒等式的有①②③④. 故选 D.
7[2023内蒙古赤峰中考]已知 $2a^{2}-a - 3 = 0$,则 $(2a + 3)(2a - 3)+(2a - 1)^{2}$ 的值是( )
A. 6
B. -5
C. -3
D. 4
A. 6
B. -5
C. -3
D. 4
答案:
D 【解析】原式$=(2a)^{2}-3^{2}+(2a)^{2}-4a + 1=2\times(2a)^{2}-4a-3^{2}+1=8a^{2}-4a-9 + 1=8a^{2}-4a-8=4(2a^{2}-a)-8$. 因为 $2a^{2}-a-3 = 0$,所以 $2a^{2}-a = 3$,所以原式$=4\times3-8 = 4$,故选 D.
8[2024上海中考]计算:$(a + b)(b - a)=$________.
答案:
$b^{2}-a^{2}$ 【解析】$(a + b)(b - a)=(b + a)(b - a)=b^{2}-a^{2}$. 故答案为 $b^{2}-a^{2}$.
9[2024四川乐山中考]已知 $a - b = 3$,$ab = 10$,则 $a^{2}+b^{2}=$________.
答案:
29 【解析】由题意知,$a^{2}+b^{2}=(a - b)^{2}+2ab=3^{2}+2\times10 = 29$. 故答案为 29.
10[2024湖南长沙中考]先化简,再求值:$2m - m(m - 2)+(m + 3)(m - 3)$,其中 $m=\frac{5}{2}$.
答案:
【解】原式$=2m-m^{2}+2m+m^{2}-9 = 4m-9$.
当 $m=\frac{5}{2}$ 时,原式$=4\times\frac{5}{2}-9 = 10-9 = 1$.
当 $m=\frac{5}{2}$ 时,原式$=4\times\frac{5}{2}-9 = 10-9 = 1$.
11[2023江苏盐城中考]先化简,再求值:$(a + 3b)^{2}+(a + 3b)(a - 3b)$,其中 $a = 2$,$b = -1$.
答案:
【解】原式$=a^{2}+6ab + 9b^{2}+a^{2}-9b^{2}=2a^{2}+6ab$.
当 $a = 2$,$b=-1$ 时,原式$=2\times2^{2}+6\times2\times(-1)=8-12=-4$.
当 $a = 2$,$b=-1$ 时,原式$=2\times2^{2}+6\times2\times(-1)=8-12=-4$.
12[2023四川凉山州中考]先化简,再求值:$(2x + y)^{2}-(2x + y)(2x - y)-2y(x + y)$,其中 $x = (\frac{1}{2})^{2023}$,$y = 2^{2022}$.
答案:
【解】原式$=4x^{2}+4xy + y^{2}-4x^{2}+y^{2}-2xy-2y^{2}=2xy$. 当 $x=(\frac{1}{2})^{2023}$,$y = 2^{2022}$ 时,原式$=2\times(\frac{1}{2})^{2023}\times2^{2022}=2\times\frac{1}{2}\times(\frac{1}{2})^{2022}\times2^{2022}=(\frac{1}{2}\times2)^{2022}=1^{2022}=1$.
查看更多完整答案,请扫码查看


