《2025年初中必刷题七年级数学下册苏科版》

三、解答题（本大题共7小题，共52分，解答应写出必要的文字说明、证明过程或推演步骤）

答案：

13（6分）[2024江苏连云港期末]计算和化简：
（1）$-2^{2}+(\pi - 2023)^{0}-(\frac{1}{2})^{-1}$.
（2）$(-2x^{2})^{3}+x^{2}\cdot x^{4}-(-3x^{3})^{2}$.
（3）先化简，再求值：$5a(a - 2)-(2a - 3)(2a + 3)-(a + 1)^{2}$，其中$a = -\frac{1}{3}$.

答案： 13. 【解】
(1)$-2^{2}+(\pi - 2023)^{0}-(\frac{1}{2})^{-1}=-4 + 1 - 2=-5$.
(2)$(-2x^{2})^{3}+x^{2}\cdot x^{4}-(-3x^{3})^{2}=-8x^{6}+x^{6}-9x^{6}=-16x^{6}$.
(3)$5a(a - 2)-(2a - 3)(2a + 3)-(a + 1)^{2}=5a^{2}-10a-4a^{2}+9-a^{2}-2a - 1=-12a + 8$.
当$a = -\frac{1}{3}$时，原式$=-12×(-\frac{1}{3})+8 = 4 + 8 = 12$.

14（6分）[2024江苏扬州期中]若$a^{m}=a^{n}(a＞0$且$a\neq1)$，则$m = n$. 利用这个结论解决下面的问题：
（1）已知$8^{2x}=2^{3x + 3}$，求x的值.
（2）若$3^{x}\times9^{x}\times27^{x}=3^{12}$，求x的值.
（3）若$x = 5^{m}-3$，$y = 4 - 25^{m}$，用含x的代数式表示y.

答案： 14. 【解】
(1)因为$8^{2x}=(2^{3})^{2x}=2^{6x}=2^{3x + 3}$，所以$6x = 3x + 3$，解得$x = 1$，所以$x$的值是 1.
(2)因为$3^{x}×9^{x}×27^{x}=3^{x}×3^{2x}×3^{3x}=3^{6x}=3^{12}$，所以$6x = 12$，解得$x = 2$，所以$x$的值是 2.
(3)因为$x = 5^{m}-3$，所以$5^{m}=x + 3$，所以$y = 4 - 25^{m}=4-(5^{2})^{m}=4-(5^{m})^{2}=4-(x + 3)^{2}$，整理，得$y=-x^{2}-6x - 5$，所以用含$x$的代数式表示$y$为$y=-x^{2}-6x - 5$.

15（6分）[2024四川宜宾期末]如图，在正方形网格中，每个小正方形的边长都为1，网格中有一个格点$\triangle ABC$（即$\triangle ABC$的顶点都在格点上）.
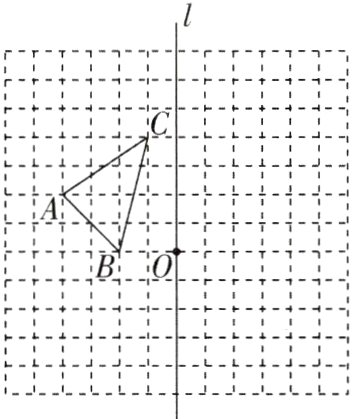
（1）画出$\triangle A_{1}B_{1}C_{1}$，使$\triangle A_{1}B_{1}C_{1}$与$\triangle ABC$关于直线l成轴对称；
（2）画出$\triangle ABC$向下平移5个单位得到的$\triangle A_{2}B_{2}C_{2}$；
（3）画出$\triangle A_{3}B_{3}C_{3}$，使$\triangle A_{3}B_{3}C_{3}$与$\triangle ABC$关于点O成中心对称.

答案：
15. 【解】
(1)如图
(1)，$\triangle A_{1}B_{1}C_{1}$即为所求.

(2)如图
(2)，$\triangle A_{2}B_{2}C_{2}$即为所求.

(3)如图
(3)，$\triangle A_{3}B_{3}C_{3}$即为所求.

本题的解题关键是根据题中给出的式子总结出规律，并能用字母表示该规律.

16（6分）[2024江苏无锡期末]学校劳动实践基地的开发能让学生体验劳动的艰辛，品味劳动成果的喜悦，满足学生劳动教育实践需要. 如图，某校劳动实践基地有两块边长分别为a，b的正方形土地A，B，其中不能使用的面积为M.
（1）用含b，M的代数式表示B中能使用的面积为________；
（2）若$a + b = 15$，$a - b = 5$，求A比B多出的使用面积.

答案： 16. 【解】
(1)因为正方形土地$B$的边长是$b$，所以$S_{B}=b^{2}$. 因为$B$中能使用的面积 = 正方形土地$B$的面积 - 不能使用的面积$M$，所以$B$中能使用的面积为$b^{2}-M$. 故答案为$b^{2}-M$.
(2)因为$a + b = 15$，$a - b = 5$，所以$A$比$B$多出的使用面积为$(a^{2}-M)-(b^{2}-M)=a^{2}-M - b^{2}+M=a^{2}-b^{2}=(a + b)(a - b)=15×5 = 75$.
答：$A$比$B$多出的使用面积为 75.