《2025年初中必刷题七年级数学下册苏科版》

1[2024山东青岛城阳区期中]计算 $(-m^{2})^{3}\cdot(2m + 1)$ 的结果是（ ）
A. $-2m^{7}-m^{6}$
B. $-2m^{6}+m^{6}$
C. $-2m^{7}-m^{5}$
D. $-2m^{6}-m^{5}$

答案： A 【解析】$(-m^{2})^{3}\cdot(2m + 1)=-m^{6}(2m + 1)=-m^{6}\cdot2m-m^{6}\cdot1=-2m^{7}-m^{6}$. 故选 A.

2[2024江苏南京期中]下列各式中，不能使用平方差公式计算的是（ ）
A. $(a + 1)(-a - 1)$
B. $(a - 1)(-a - 1)$
C. $(a + 1)(a - 1)$
D. $(a + 1)(1 - a)$

答案：
A 【解析】
A $(a + 1)(-a - 1)=-(a + 1)^{2}$，不能使用平方差公式计算，故此选项符合题意
B $(a - 1)(-a - 1)=-(a - 1)(a + 1)$，能使用平方差公式计算，故此选项不符合题意
C $(a + 1)(a - 1)$能使用平方差公式计算，故此选项不符合题意
D $(a + 1)(1 - a)$能使用平方差公式计算，故此选项不符合题意

3[2024江苏南通期中]已知 $a - b + 2 = 5$，则代数式 $a^{2}-b^{2}-6b$ 的值为（ ）
A. 3
B. 6
C. 9
D. 12

答案： C 【解析】因为 $a - b+2 = 5$，所以 $a - b = 3$，所以 $a^{2}-b^{2}-6b=(a - b)(a + b)-6b=3(a + b)-6b=3a + 3b-6b=3a-3b=3(a - b)=3\times3 = 9$. 故选 C.

4若 $x^{2}-2(m + 1)x + 144$ 是完全平方式，则常数 $m$ 的值为（ ）
A. -11或13
B. 11或-13
C. $\pm11$
D. $\pm13$

答案： B 【解析】因为 $x^{2}-2(m + 1)x + 144$ 是完全平方式，所以 $m + 1=\pm12$，解得 $m = 11$ 或 -13，故选 B.

5已知 $a$，$b$，$c$ 是三角形的三条边长，那么代数式 $(a - b)^{2}-c^{2}$ 的值（ ）
A. 大于0
B. 等于0
C. 小于0
D. 无法确定

答案： C 【解析】因为 $a$，$b$，$c$ 是三角形的三条边长，所以 $a + c＞b$，$b + c＞a$，所以 $a - b + c＞0$，$a - b - c＜0$，所以 $(a - b)^{2}-c^{2}=(a - b + c)(a - b - c)＜0$，故选 C.

6若 $a^{2}+2ab + b^{2}-c^{2}=10$，$a + b + c = 5$，则 $a + b - c$ 的值是（ ）
A. 2
B. 5
C. 20
D. 9

答案： A 【解析】由 $a^{2}+2ab + b^{2}-c^{2}=10$，得 $(a + b)^{2}-c^{2}=10$，则 $(a + b + c)(a + b - c)=10$. 因为 $a + b + c = 5$，所以 $5(a + b - c)=10$，解得 $a + b - c = 2$.

7[2024河北邯郸模拟]已知 $4^{8}-1=(4^{4}+1)(4^{4}-1)$，最后可推算出 $4^{8}-1$ 的结果一定能（ ）
A. 被12整除
B. 被13整除
C. 被14整除
D. 被15整除

答案： D 【解析】$4^{8}-1=(4^{4}+1)(4^{4}-1)=(4^{4}+1)(4^{2}+1)(4^{2}-1)=(4^{4}+1)(4^{2}+1)\times15$，即 $4^{8}-1$ 的结果一定能被 15 整除. 故选 D.

8[2024江苏常州天宁区期中]如果一个正整数能表示为两个连续奇数的平方差，那么我们称这个数为“幸福数”. 因为 $16 = 5^{2}-3^{2}$，所以16就是“幸福数”. 下列数中为“幸福数”的是（ ）
A. 520
B. 502
C. 250
D. 205

答案： A 【解析】设两个连续奇数分别为 $2a - 1$，$2a + 1$（$a$ 为正整数），则 $(2a + 1)^{2}-(2a - 1)^{2}=(2a + 1+2a - 1)(2a + 1-2a + 1)=4a\times2 = 8a$. 令 $8a = 520$，解得 $a = 65$，所以 520 是“幸福数”；令 $8a = 502$，解得 $a = 62.75$（不符合题意，舍去），所以 502 不是“幸福数”；令 $8a = 250$，解得 $a = 31.25$（不符合题意，舍去），所以 250 不是“幸福数”；令 $8a = 205$，解得 $a = 25.625$（不符合题意，舍去），所以 205 不是“幸福数”. 故选 A.

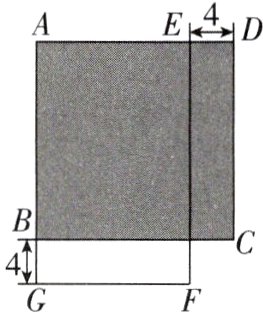
9[2024江苏苏州期中]某小区内有一块正方形草坪 $ABCD$，如图所示，小区物业现对该草坪进行改造，将该正方形草坪的 $AB$ 边增加4米，$AD$ 边减少4米，则改造后的长方形草坪 $AEFG$ 的面积与原来正方形草坪 $ABCD$ 的面积相比（ ）

A. 增加8平方米
B. 增加16平方米
C. 减少16平方米
D. 保持不变

答案： C 【解析】设正方形草坪 $ABCD$ 的边长为 $x$ 米. 由题意可知 $AE=x - 4$，$AG=x + 4$，所以 $S_{正方形ABCD}=x^{2}$，$S_{长方形AEFG}=(x + 4)(x - 4)=x^{2}-16$，所以 $S_{正方形ABCD}-S_{长方形AEFG}=x^{2}-(x^{2}-16)=16$，即改造后的长方形草坪 $AEFG$ 的面积与原来正方形草坪 $ABCD$ 的面积相比减少 16 平方米. 故选 C.

10已知 $a^{2}+3a + 1 = 0$，则 $6 - 3a^{2}-9a$ 的值为________.

答案： 9 【解析】由 $a^{2}+3a + 1 = 0$，得 $a^{2}+3a=-1$，则原式$=6-3(a^{2}+3a)=9$.

11[2024江苏扬州期中]已知多项式 $x^{2}+mx + 4$ 是完全平方式，则 $m$ 的值为________.

答案： $\pm4$ 【解析】因为 $x^{2}+mx + 4=x^{2}+mx+(\pm2)^{2}$ 是完全平方式，所以 $mx=2\cdot x\cdot(\pm2)=\pm4x$，所以 $m=\pm4$. 故答案为 $\pm4$.

12[2024江苏泰州期中]已知 $x^{2}-3x + 5=(x - 2)^{2}+a(x - 2)+b$，则 $a + b=$________.

答案： 4 【解析】$x^{2}-3x + 5=(x - 2)^{2}+a(x - 2)+b=x^{2}-4x + 4+ax-2a + b=x^{2}+(a - 4)x-2a + b + 4$，所以 $a - 4=-3$，$-2a + b + 4 = 5$，所以 $a = 1$，$b = 3$，所以 $a + b = 4$. 故答案为 4.

13[2024江苏泰州姜堰区调研]要使 $(-2x^{2}+mx + 1)\cdot(-3x^{2})$ 的结果中不含 $x^{3}$ 项，则 $m=$________.

答案： 0 【解析】$(-2x^{2}+mx + 1)\cdot(-3x^{2})=-2x^{2}\times(-3x^{2})+mx\times(-3x^{2})+1\times(-3x^{2})=6x^{4}-3mx^{3}-3x^{2}$. 因为结果中不含 $x^{3}$ 项，所以 $-3m = 0$，所以 $m = 0$. 故答案为 0.

14[2024河南郑州期中]运用乘法公式简便计算：$2024^{2}-2025\times2023=$________.

答案： 1 【解析】$2024^{2}-2025\times2023=2024^{2}-(2024 + 1)\times(2024 - 1)=2024^{2}-(2024^{2}-1)=2024^{2}-2024^{2}+1 = 1$. 故答案为 1.

15[新考向开放性试题][2024河北沧州模拟]已知整式 $A = 1 + 2x$，整式 $B = 1 - 2x$. 若 $A\cdot B + M$ 是关于 $x$ 的一个完全平方式，写出一个满足条件的整式 $M$：________.

答案： $4x-2$（答案不唯一） 【解析】由题可得 $A\cdot B+M=(1 + 2x)(1 - 2x)+M=-4x^{2}+M + 1$. 因为 $A\cdot B+M$ 是关于 $x$ 的一个完全平方式，所以 $M$ 可以为 $4x-2$，此时原式$=-4x^{2}+4x-2 + 1=-(4x^{2}-4x + 1)=-(2x - 1)^{2}$，所以整式 $M$ 可以是 $4x-2$. 故答案为 $4x-2$（答案不唯一）.

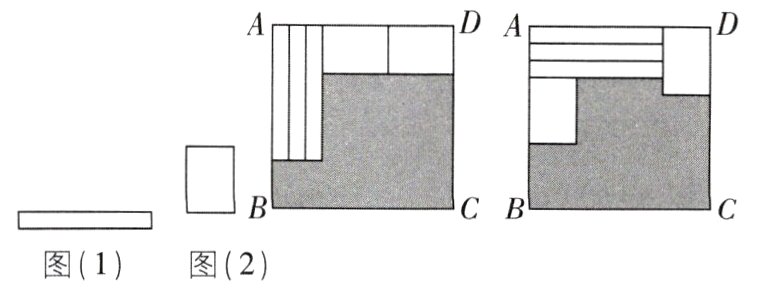
16如图，用三个图(1)中的长方形和两个图(2)中的长方形按照两种方式去覆盖一个大的长方形 $ABCD$，两种方式未覆盖的部分（阴影部分）的周长一样，那么图(1)中长方形的面积 $S_{1}$ 与图(2)中长方形的面积 $S_{2}$ 的比值是________.

答案： $\frac{2}{3}$ 【解析】设题图（1）中长方形的长为 $a$，宽为 $b$，题图（2）中长方形的长为 $y$，宽为 $x$，则 $AD=3b + 2y=a + x$. 第一种覆盖方式中阴影部分的周长为 $2(3b + 2y+DC - x)=2(a + x+DC - x)=2a + 2DC$. 第二种覆盖方式中阴影部分的周长为 $2(a + x+DC - 3b)=2a + 2x+2DC-6b=2a + 2x+2DC-2(a + x - 2y)=2DC + 4y$. 因为两种方式阴影部分周长一样，所以 $2a + 2DC=2DC + 4y$，所以 $a = 2y$. 因为 $3b + 2y=a + x$，所以 $x = 3b$，所以 $\frac{S_{1}}{S_{2}}=\frac{ab}{xy}=\frac{2y\cdot\frac{x}{3}}{xy}=\frac{2}{3}$. 故答案为 $\frac{2}{3}$.