《2025年初中必刷题七年级数学下册苏科版》

1[2024江苏常州质检]若$x^{2}+4x+k=(x + 2)^{2}$，则常数$k$的值是（ ）
A. 2
B. 4
C. 1
D. -4

答案： B　[解析]因为$x^{2}+4x+k=(x + 2)^{2}=x^{2}+4x + 4$，所以$k = 4$. 故选B.

2[2024四川成都期中]利用完全平方公式计算$(-x - 2y)^{2}$的结果为（ ）
A. $-x^{2}-2xy - 4y^{2}$
B. $-x^{2}-4xy - 4y^{2}$
C. $x^{2}-4xy + 4y^{2}$
D. $x^{2}+4xy + 4y^{2}$

答案： D　[解析]$(-x - 2y)^{2}=x^{2}+4xy + 4y^{2}$. 故选D.

3若$(ax - y)^{2}=4x^{2}-4xy + by^{2}$，则$a$，$b$的值分别为（ ）
A. 2，1
B. -2，1
C. -2，-1
D. 4，1

答案： A　[解析]因为$(ax - y)^{2}=a^{2}x^{2}-2axy + y^{2}=4x^{2}-4xy + by^{2}$，所以$a^{2}=4$，$-2a=-4$，$b = 1$，解得$a = 2$，$b = 1$. 故选A.

4已知$(a + b)^{2}=7$，$(a - b)^{2}=4$，则$ab$的值为（ ）
A. $\frac{1}{4}$
B. $\frac{1}{2}$
C. $\frac{3}{4}$
D. $\frac{5}{4}$

答案： 4.C　[解析]$(a + b)^{2}-(a - b)^{2}=a^{2}+2ab + b^{2}-a^{2}+2ab - b^{2}=4ab = 3$，则$ab=\frac{3}{4}$.

5[2024江苏常州期中]已知一个正方形的边长是$a$，若它的边长增加1，则这个正方形的面积增加（ ）
A. 1
B. $2a + 1$
C. $a^{2}$
D. $a^{2}+2a + 1$

答案： 5.B　[解析]因为新正方形的边长为$a + 1$，所以这个正方形的面积增加$(a + 1)^{2}-a^{2}=a^{2}+2a + 1 - a^{2}=2a + 1$. 故选B.

6[2024浙江绍兴期中]若$x^{2}+xy = 17 - a$，$y^{2}+xy = 8 + a$，则$x + y=$________.

答案： 6. $\pm5$ [解析]因为$x^{2}+xy = 17 - a$，$y^{2}+xy = 8 + a$，所以$x^{2}+xy + y^{2}+xy = x^{2}+2xy + y^{2}=8 + a + 17 - a$，即$(x + y)^{2}=25$，解得$x + y=\pm5$. 故答案为$\pm5$.

7用简便方法计算：
（1）$101^{2}$； （2）$999^{2}$.

答案： 7. [解]
(1)$101^{2}=(100 + 1)^{2}=10000 + 200 + 1 = 10201$.
(2)$999^{2}=(1000 - 1)^{2}=1000000 - 2000 + 1 = 998001$.

8(1)已知$x + y = 3$，$xy = 2$，分别求$x^{2}+y^{2}$，$(x - y)^{2}$，$x^{4}+y^{4}$的值；
(2)已知$x + 2y = 3$，$xy = 1$，求$x^{2}-xy + 4y^{2}$的值.

答案： 8. [解]
(1) 因为$x + y = 3$，$xy = 2$，所以$x^{2}+y^{2}=(x + y)^{2}-2xy = 3^{2}-2\times2 = 5$，$(x - y)^{2}=x^{2}-2xy + y^{2}=(x + y)^{2}-4xy = 3^{2}-4\times2 = 1$，$x^{4}+y^{4}=(x^{2}+y^{2})^{2}-2x^{2}y^{2}=5^{2}-2\times2^{2}=17$.
(2) 因为$x + 2y = 3$，$xy = 1$，所以$x^{2}-xy + 4y^{2}=(x + 2y)^{2}-5xy = 3^{2}-5\times1 = 4$.

9有一张边长为$a$厘米的正方形桌面，因为实际需要，需将该正方形桌面的边长增加$b$厘米，木工师傅设计了如图所示的三种方案：

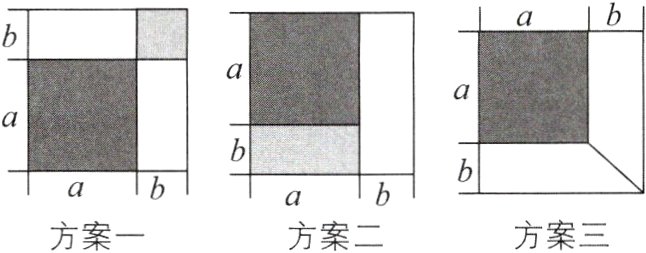
小明发现这三种方案都能验证公式：$(a + b)^{2}=a^{2}+2ab + b^{2}$.
对于方案一，小明是这样验证的：$a^{2}+ab + ab + b^{2}=a^{2}+2ab + b^{2}=(a + b)^{2}$.
请你根据方案二、方案三，写出公式的验证过程.
方案二： 方案三：

答案： 9. [解]方案二：$a^{2}+ab+(a + b)b=a^{2}+ab + ab + b^{2}=a^{2}+2ab + b^{2}=(a + b)^{2}$.
方案三：$a^{2}+\frac{[a+(a + b)]b}{2}+\frac{[a+(a + b)]b}{2}=a^{2}+ab+\frac{1}{2}b^{2}+ab+\frac{1}{2}b^{2}=a^{2}+2ab + b^{2}=(a + b)^{2}$.

10[2024江苏盐城期中]若$x^{2}+(k - 2)x + 9$是完全平方式，则$k$的值为（ ）
A. 6
B. -4或8
C. -6或6
D. 0

答案： 10.B　[解析]因为$x^{2}+(k - 2)x + 9$是完全平方式，所以$x^{2}+(k - 2)x + 9 = x^{2}+(k - 2)x + 3^{2}=(x\pm3)^{2}=x^{2}\pm6x + 9$，所以$k - 2 = 6$或$k - 2=-6$，解得$k=-4$或$k = 8$. 故选B.