第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1[2023江苏扬州期中,中]若$x^{2}+y^{2}=(x + y)^{2}+A=(x - y)^{2}-B$,则$A$与$B$的数量关系为( )
A. 相等
B. 互为相反数
C. 互为倒数
D. 无法确定
A. 相等
B. 互为相反数
C. 互为倒数
D. 无法确定
答案:
1.A [解析]因为$x^{2}+y^{2}=(x + y)^{2}+(-2xy)=(x - y)^{2}-(-2xy)$,所以$A=-2xy$,$B=-2xy$,所以$A = B$,故选A.
2[2024江苏宿迁质检,中]若$(x - 2023)^{2}+(x - 2025)^{2}=26$,则$(x - 2024)^{2}$的值是( )
A. 4
B. 8
C. 12
D. 16
A. 4
B. 8
C. 12
D. 16
答案:
2.C [解析]设$x - 2024 = a$. 因为$(x - 2023)^{2}+(x - 2025)^{2}=26$,所以$(a + 1)^{2}+(a - 1)^{2}=26$,所以$a^{2}+2a + 1 + a^{2}-2a + 1 = 26$,所以$2a^{2}+2 = 26$,所以$a^{2}=12$,所以$(x - 2024)^{2}=12$. 故选C.
3新考法[中]设$a$,$b$是有理数,定义$*$的一种运算如下:$a*b=(a + b)^{2}$,则下列结论:①$a*b = 0$,则$a = 0$且$b = 0$;②$a*b = b*a$;③$a*(b + c)=a*b + a*c$;④$a*b=(-a)*(-b)$,正确的有( )
A. 1个
B. 2个
C. 3个
D. 4个
A. 1个
B. 2个
C. 3个
D. 4个
答案:
3.B [解析]因为$a*b = 0$,$a*b=(a + b)^{2}$,所以$(a + b)^{2}=0$,即$a + b = 0$,所以$a$,$b$互为相反数,故①不符合题意. $a*b=(a + b)^{2}$,$b*a=(b + a)^{2}$,故②符合题意. $a*(b + c)=(a + b + c)^{2}=a^{2}+ab + ac + ab + b^{2}+bc + ac + bc + c^{2}=a^{2}+b^{2}+c^{2}+2ab + 2ac + 2bc$,$a*b + a*c=(a + b)^{2}+(a + c)^{2}=a^{2}+2ab + b^{2}+a^{2}+2ac + c^{2}=2a^{2}+b^{2}+c^{2}+2ab + 2ac$,故③不符合题意. 因为$a*b=(a + b)^{2}$,$(-a)*(-b)=(-a - b)^{2}$,$(a + b)^{2}=(-a - b)^{2}$,所以$a*b=(-a)*(-b)$,故④符合题意,因此正确的有 2 个,故选B.
4[较难]已知有理数$x$,$y$,$z$满足$x^{2}+y^{2}+z^{2}=4$,则$(2x - y)^{2}+(2y - z)^{2}+(2z - x)^{2}$的最大值是( )
A. 12
B. 20
C. 28
D. 36
A. 12
B. 20
C. 28
D. 36
答案:
4.C [解析]因为有理数$x$,$y$,$z$满足$x^{2}+y^{2}+z^{2}=4$,所以$(2x - y)^{2}+(2y - z)^{2}+(2z - x)^{2}=5(x^{2}+y^{2}+z^{2})-4(xy + yz + xz)=20-2[(x + y + z)^{2}-(x^{2}+y^{2}+z^{2})]=28-2(x + y + z)^{2}\leq28$,所以当$x + y + z = 0$时,$(2x - y)^{2}+(2y - z)^{2}+(2z - x)^{2}$有最大值,是 28. 故选C.
5[中]若$25x^{2}+1$加上一个单项式能成为二次三项式,且是一个完全平方式,这个单项式是________.
答案:
5. $10x$或$-10x$或$\frac{625}{4}x^{4}$ [解析]①$25x^{2}$是平方项时,$25x^{2}\pm10x + 1=(5x\pm1)^{2}$,所以可添加的项是$10x$或$-10x$;②$25x^{2}$是乘积二倍项时,$\frac{625}{4}x^{4}+25x^{2}+1=(\frac{25}{2}x^{2}+1)^{2}$,所以可添加的项是$\frac{625}{4}x^{4}$. 综上所述,可添加的项是$10x$或$-10x$或$\frac{625}{4}x^{4}$. 故答案为$10x$或$-10x$或$\frac{625}{4}x^{4}$.
6新考法[2023四川成都期中,中]已知$(x + y)^{2}$的展开式为$x^{2}+2xy + y^{2}$,即$(x + y)^{2}=x^{2}+2xy + y^{2}$,则要想知道$(x - y)^{2}$的展开式,可以将$(x - y)^{2}$看成$[x+( - y)]^{2}$,那么可得$(x - y)^{2}=[x+( - y)]^{2}=x^{2}+2\cdot x\cdot( - y)+y^{2}=x^{2}-2xy + y^{2}$. 根据上述材料写出$(2x - 3y - z)^{2}$的展开式:________.
答案:
6. $4x^{2}+9y^{2}+z^{2}-12xy + 6yz - 4xz$ [解析]$(2x - 3y - z)^{2}=[(2x - 3y)+(-z)]^{2}=(2x - 3y)^{2}+2\cdot(2x - 3y)\cdot(-z)+(-z)^{2}=[2x+(-3y)]^{2}-4xz + 6yz - z^{2}=4x^{2}+2\cdot2x\cdot(-3y)+(-3y)^{2}-4xz + 6yz - z^{2}=4x^{2}+9y^{2}+z^{2}-12xy + 6yz - 4xz$.
7[2024浙江衢州期末,中]若有理数$a$,$b$,$c$满足$a^{2}+b^{2}+c^{2}+4 = ab + 3b + 2c$,则$200a + 9b + c=$________.
答案:
7. 219 [解析]因为$a^{2}+b^{2}+c^{2}+4 = ab + 3b + 2c$,所以$a^{2}+b^{2}+c^{2}+4 - ab - 3b - 2c = 0$,$a^{2}-ab+\frac{b^{2}}{4}+(\frac{3b^{2}}{4}-3b + 3)+(c^{2}-2c + 1)=0$,即$(a-\frac{b}{2})^{2}+\frac{3}{4}(b - 2)^{2}+(c - 1)^{2}=0$. 因为$(a-\frac{b}{2})^{2}\geq0$,$(b - 2)^{2}\geq0$,$(c - 1)^{2}\geq0$,所以$a-\frac{b}{2}=0$,$b - 2 = 0$,$c - 1 = 0$,解得$a = 1$,$b = 2$,$c = 1$,所以$200a + 9b + c = 200\times1+9\times2+1 = 219$. 故答案为 219.
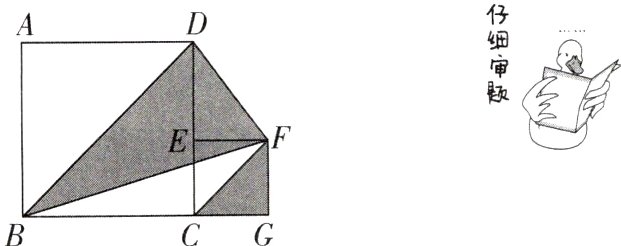
8[2024浙江宁波期末,较难]如图,已知四边形$ABCD$,四边形$ECGF$都是正方形,$\triangle BCF$的面积为5,$BG$的长为7,则阴影部分的面积是________.

答案:
8. 14.5 [解析]因为四边形$ABCD$,四边形$ECGF$都是正方形,所以$\angle A=\angle G = 90^{\circ}$,$AD = AB = BC = CD$,$CG = FG$,所以$S_{\triangle BCF}=\frac{1}{2}BC\cdot FG = 5$,所以$BC\cdot FG = 10$. 因为$BG = BC + CG = 7$,所以$BC^{2}+CG^{2}=(BC + CG)^{2}-2BC\cdot CG = 49-2\times10 = 29$,所以$S_{正方形ABCD}+S_{正方形CEFG}=29$. 因为$S_{\triangle DEF}=\frac{1}{2}EF\cdot DE=\frac{1}{2}CG\cdot(AB - CG)=\frac{1}{2}CG\cdot AB-\frac{1}{2}CG^{2}=5-\frac{1}{2}CG^{2}$,所以阴影部分的面积为$S_{正方形ABCD}+S_{正方形CEFG}+S_{\triangle DEF}-S_{\triangle ABD}-S_{\triangle BCF}=29 + 5-\frac{1}{2}CG^{2}-\frac{1}{2}AB^{2}-5=29-\frac{1}{2}(CG^{2}+AB^{2})=29-\frac{1}{2}\times29 = 14.5$. 故答案为 14.5.
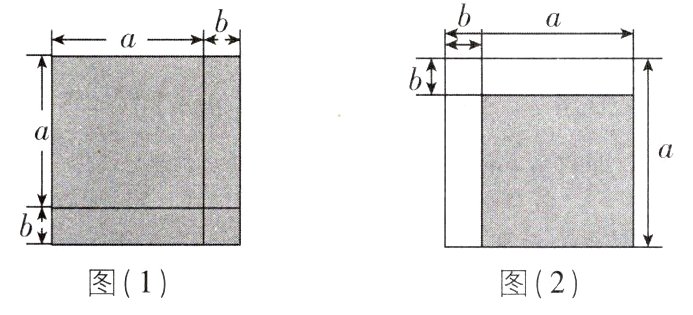
9核心素养·几何直观[较难](1)分别计算图(1)、图(2)、图(3)中阴影部分的面积,并写出关于$a$,$b$的等量关系式.
(2)尝试解决:①已知$m + n = 2$,$m^{2}+n^{2}=7$,则$mn=$________;
②已知$2a + b = 3$,$ab = 1$,求$(2a - b)^{2}$的值;
③已知$(4 - x)(5 - x)=6$,求$(4 - x)^{2}+(5 - x)^{2}$的值.
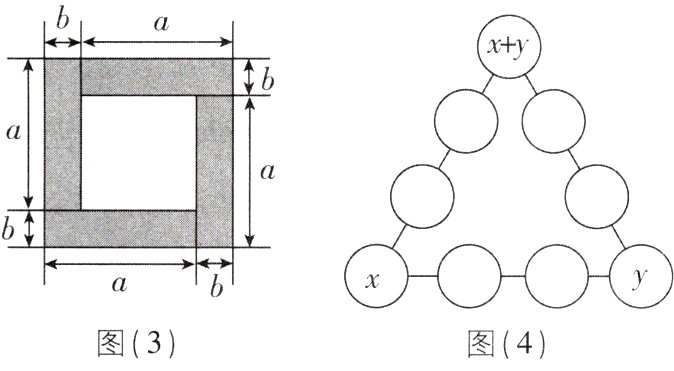
(3)填数游戏:如图(4),把数字1~9填入构成三角形的9个圆圈中,使得各边上的四个数字的和都等于21,将每边四个数字的平方和分别记为$A$,$B$,$C$,已知$A + B + C = 411$. 如果将位于这个三角形顶点处的三个圆圈填入的数字分别表示为$x$,$y$,$x + y$,求$xy$的值.
(2)尝试解决:①已知$m + n = 2$,$m^{2}+n^{2}=7$,则$mn=$________;
②已知$2a + b = 3$,$ab = 1$,求$(2a - b)^{2}$的值;
③已知$(4 - x)(5 - x)=6$,求$(4 - x)^{2}+(5 - x)^{2}$的值.
(3)填数游戏:如图(4),把数字1~9填入构成三角形的9个圆圈中,使得各边上的四个数字的和都等于21,将每边四个数字的平方和分别记为$A$,$B$,$C$,已知$A + B + C = 411$. 如果将位于这个三角形顶点处的三个圆圈填入的数字分别表示为$x$,$y$,$x + y$,求$xy$的值.


答案:
9. [解]
(1) 由题图
(1) 可得阴影部分面积既可以表示为$(a + b)^{2}$,又可以表示为$a^{2}+2ab + b^{2}$,则$(a + b)^{2}=a^{2}+2ab + b^{2}$;由题图
(2) 可得阴影部分面积既可以表示为$(a - b)^{2}$,又可以表示为$a^{2}-2ab + b^{2}$,则$(a - b)^{2}=a^{2}-2ab + b^{2}$;由题图
(3) 可得阴影部分面积既可以表示为$4ab$,又可以表示为$(a + b)^{2}-(a - b)^{2}$,则$4ab=(a + b)^{2}-(a - b)^{2}$.
(2) ①因为$m + n = 2$,所以$(m + n)^{2}=m^{2}+2mn + n^{2}=4$. 因为$m^{2}+n^{2}=7$,所以$7 + 2mn = 4$,所以$mn=-\frac{3}{2}$,故答案为$-\frac{3}{2}$.
②因为$ab = 1$,所以$8ab = 8$. 因为$(2a - b)^{2}=(2a + b)^{2}-8ab$,$2a + b = 3$,$8ab = 8$,所以$(2a - b)^{2}=3^{2}-8 = 1$.
③因为$(4 - x)-(5 - x)=-1$,所以$[(4 - x)-(5 - x)]^{2}=1$. 因为$(4 - x)(5 - x)=6$,所以$(4 - x)^{2}+(5 - x)^{2}=1+2(4 - x)(5 - x)=1 + 12 = 13$.
(3) 数字$1\sim9$的和为$1+2+3+4+5+6+7+8+9 = 45$.
因为各边上的四个数字的和都等于 21,所以$21\times3-45 = 18$,所以$x + y+(x + y)=18$,即$x + y = 9$.
因为每边四个数字的平方和分别记为$A$,$B$,$C$,满足$A + B + C = 411$,且$1^{2}+2^{2}+3^{2}+4^{2}+5^{2}+6^{2}+7^{2}+8^{2}+9^{2}=285$,所以$x^{2}+y^{2}+(x + y)^{2}=126$,所以$x^{2}+y^{2}+81 = 126$,所以$x^{2}+y^{2}=45$,所以$(x + y)^{2}-2xy = 45$,所以$xy = 18$.
(1) 由题图
(1) 可得阴影部分面积既可以表示为$(a + b)^{2}$,又可以表示为$a^{2}+2ab + b^{2}$,则$(a + b)^{2}=a^{2}+2ab + b^{2}$;由题图
(2) 可得阴影部分面积既可以表示为$(a - b)^{2}$,又可以表示为$a^{2}-2ab + b^{2}$,则$(a - b)^{2}=a^{2}-2ab + b^{2}$;由题图
(3) 可得阴影部分面积既可以表示为$4ab$,又可以表示为$(a + b)^{2}-(a - b)^{2}$,则$4ab=(a + b)^{2}-(a - b)^{2}$.
(2) ①因为$m + n = 2$,所以$(m + n)^{2}=m^{2}+2mn + n^{2}=4$. 因为$m^{2}+n^{2}=7$,所以$7 + 2mn = 4$,所以$mn=-\frac{3}{2}$,故答案为$-\frac{3}{2}$.
②因为$ab = 1$,所以$8ab = 8$. 因为$(2a - b)^{2}=(2a + b)^{2}-8ab$,$2a + b = 3$,$8ab = 8$,所以$(2a - b)^{2}=3^{2}-8 = 1$.
③因为$(4 - x)-(5 - x)=-1$,所以$[(4 - x)-(5 - x)]^{2}=1$. 因为$(4 - x)(5 - x)=6$,所以$(4 - x)^{2}+(5 - x)^{2}=1+2(4 - x)(5 - x)=1 + 12 = 13$.
(3) 数字$1\sim9$的和为$1+2+3+4+5+6+7+8+9 = 45$.
因为各边上的四个数字的和都等于 21,所以$21\times3-45 = 18$,所以$x + y+(x + y)=18$,即$x + y = 9$.
因为每边四个数字的平方和分别记为$A$,$B$,$C$,满足$A + B + C = 411$,且$1^{2}+2^{2}+3^{2}+4^{2}+5^{2}+6^{2}+7^{2}+8^{2}+9^{2}=285$,所以$x^{2}+y^{2}+(x + y)^{2}=126$,所以$x^{2}+y^{2}+81 = 126$,所以$x^{2}+y^{2}=45$,所以$(x + y)^{2}-2xy = 45$,所以$xy = 18$.
查看更多完整答案,请扫码查看


