《2025年初中必刷题七年级数学下册苏科版》

1. 某商品进价15元，标价20元. 为了促销，现决定打折销售，但每件利润不少于3元，则最多可以打　　　　　　　　　　　　　　　(　　　)
A. 6折　　
　B. 7折　　
　C. 8折　　
　D. 9折

答案： D 【解析】设可以打x折销售. 依题意得$20\times\frac{x}{10}-15\geq3$，解得$x\geq9$. 故选 D.

2. 某公司推出两种手机通话费用收费方案. 方案一：月租费36元，本地通话费为0.1元/分；方案二：不收月租费，本地通话费为0.6元/分. 若小明爸爸选择方案一比方案二优惠，则他一个月通话时间可能为　　　　　　　　(　　　)
A. 60分钟　　　　　　
　B. 70分钟
C. 72分钟　　　　　　
　D. 80分钟

答案： D 【解析】设小明爸爸一个月通话时间为x分钟. 方案一费用为$(36 + 0.1x)$元，方案二费用为$0.6x$元，方案一比方案二优惠时，$36 + 0.1x＜0.6x$，解得$x＞72$.

3. 甲、乙两人从相距24km的A、B两地沿着同一条公路相向而行，若甲的速度是乙的速度的两倍，且要保证在2h以内（不包含2h）相遇，则甲的速度　　　　　　　　　　　　　　(　　　)
A. 小于8km/h　　　　
　B. 大于8km/h
C. 小于4km/h　　　　
　D. 大于4km/h

答案： B 【解析】设甲的速度为$x$ km/h，则乙的速度为$\frac{1}{2}x$ km/h. 由已知得$2\times(x+\frac{1}{2}x)＞24$，解得$x＞8$. 故选 B.
关键点拔：解本题的关键是正确理解新定义.
思路分析：
(1)设该参赛同学一共答对了x道题，答错了y道题，根据总题数为25及总得分 = 4×答对题数 - 1×答错题数，列出二元一次方程组，解方程组即可；
(2)设参赛者答对m道题，则答错了$(25 - m)$道题，根据总得分 = 4×答对题数 - 1×答错题数，结合总得分大于或等于92分，列出一元一次不等式，即可求解.

4. 斑马线前“车让人”，反映了城市的文明程度，但行人一般都会在红灯亮起前通过马路. 某人行横道全长24米，小明以1.2米/秒的速度过该人行横道，行至$\frac{1}{3}$处时，9秒倒计时灯亮了. 小明要在红灯亮起前通过马路，他的速度至少要提高到原来的　　　　　　　　　　(　　　)
A. 1.1倍　　　　　　
　B. 1.4倍
C. 1.5倍　　　　　　
　D. 1.6倍

答案： C 【解析】设他的速度要提高到原来的x倍. 根据题意可得$9\times1.2x\geq24\times(1 - \frac{1}{3})$，解得$x\geq\frac{40}{27}$. 因为$\frac{40}{27}\approx1.48$，所以他的速度至少要提高到原来的1.5倍. 故选 C.

5. 三个连续正整数的和不大于33，这样的正整数有__________组.

答案： 10 【解析】设三个连续正整数中最小的数为x，则另外两个数分别为$x + 1$，$x + 2$. 依题意得$x + x + 1 + x + 2\leq33$，解得$x\leq10$. 又因为x为正整数，所以x可以为1，2，3，4，5，6，7，8，9，10，所以这样的正整数有10组. 故答案为10.

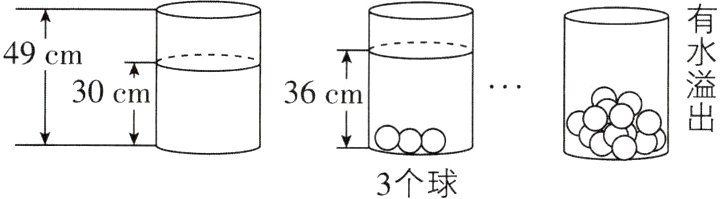
6. （新考法）小菲受《乌鸦喝水》故事的启发，利用量筒和体积相同的小球进行了如图所示的操作，根据图中给出的信息，量筒中至少放入________个小球时有水溢出.
建议用时40分钟答案D53
　

答案： 10 【解析】由题意得，每加1个球，水面上升$(36 - 30)\div3 = 2(cm)$. 设放入x个小球时有水溢出，则$2x + 30＞49$，解得$x＞9.5$. 因为x为整数，所以至少放入10个小球时有水溢出. 故答案为10.

7. 为庆祝中国共青团成立100周年，发扬红色传统，传承红色精神，某学校举行了主题为“学史明理，学史增信，学史崇德，学史力行”的党史知识竞赛，一共有25道题，满分100分，每一题答对得4分，答错扣1分，不答得0分.
　(1)列二元一次方程组解决下列问题：若某参赛同学只有一道题没有作答，最后他的总得分为81分，则该参赛同学一共答对了多少道题？
　(2)若规定参赛者每道题都必须作答且总得分大于或等于92分才可以被评为“学党史小达人”，则参赛者至少需答对多少道题才能被评为“学党史小达人”？
　　　　　　　　　　　　　　

答案： 【解】
(1)设该参赛同学一共答对了x道题，答错了y道题.
依题意得$\begin{cases}x + y + 1 = 25\\4x - y = 81\end{cases}$，解得$\begin{cases}x = 21\\y = 3\end{cases}$.
答：该参赛同学一共答对了21道题.
(2)设参赛者答对m道题，则答错了$(25 - m)$道题. 依题意得$4m-(25 - m)\geq92$，解得$m\geq23.4$. 因为m为正整数，所以m的最小值为24.
答：参赛者至少需答对24道题才能被评为“学党史小达人”.