《2025年初中必刷题七年级数学下册苏科版》

1[2024江苏苏州吴江区期末,中]教室里的水平地面上有一个倒地的灰斗，如图为它的示意图，BC与地面的夹角为55°,∠BCD = 26°,小明同学将它扶起(将灰斗绕点C逆时针旋转)后平放在地面上,AB的对应线段为A'B',在这一过程中,灰斗柄AB绕点C旋转了（　　）

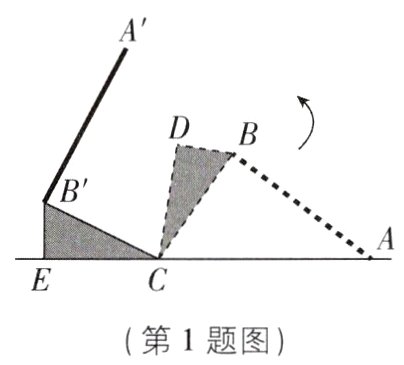
A. 99°　　　　　　　
　B. 89°
C. 74°　　　　　　　
　D. 64°

答案： A【解析】由题意可得，∠BCA = 55°，∠BCD = ∠ECB' = 26°，所以∠B'CD = 180° - 26°×2 - 55° = 73°，所以旋转角∠BCB' = ∠B'CD + ∠BCD = 73° + 26° = 99°. 故选A.

2[2024上海普陀区期末,中]如图,在△ABC中,∠ACB = 50°,将△ABC绕点C逆时针旋转得到△DEC(点D,E分别与点A,B对应),如果∠ACD 与∠ACE的度数之比为3:2,当旋转角大于0°且小于180°时,旋转角的度数为________.

答案：
30°或150°【解析】当旋转角小于50°时，如图
(1). 因为∠ACB = 50°，△ABC绕点C逆时针旋转得到△DEC，所以∠DCE = 50°. 因为∠ACD与∠ACE的度数之比为3:2，所以旋转角∠ACD = $\frac{3}{3 + 2}$×50° = 30°. 当旋转角大于50°时，如图
(2). 因为∠ACD与∠ACE的度数之比为3:2，∠DCE = ∠ACB = 50°，所以∠ACE = 2∠DCE = 100°，所以旋转角∠BCE = ∠ACB + ∠ACE = 150°. 故答案为30°或150°.
　　

3[2024江苏泰州调研,中]将线段AB绕点O逆时针旋转60°,得到对应线段A'B',请用无刻度的直尺及圆规作图.(保留作图的痕迹,不要求写出作法)
（1）作出旋转中心O；
（2）作出线段A'B'.

答案：
【解】
(1)如图，连接AA'，在AA'的上方分别以点A、点A'为圆心，AA'的长为半径画弧，两弧交于点O，点O即为所求.

(2)如图，连接OB，分别以点B、点O为圆心，OB的长为半径画弧，两弧交于点B'，连接A'B'，线段A'B'即为所求.

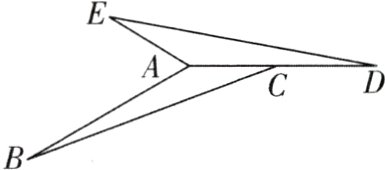
4[2024江苏盐城期中,中]如图,在△ABC中,∠B + ∠ACB = 30°,AB = 4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD 中点.
（1）指出旋转中心,并求出旋转角的度数.
（2）求出∠BAE的度数和AE的长.

答案： 【解】
(1)在△ABC中，因为∠B + ∠ACB = 30°，所以∠BAC = 150°.
因为△ABC逆时针旋转一定角度后与△ADE重合，所以旋转中心为点A，∠BAD等于旋转角，即旋转角为150°.
(2)因为△ABC绕点A逆时针旋转150°后与△ADE重合，所以∠DAE = ∠BAC = 150°，AB = AD = 4，AC = AE，所以∠BAE = 360° - 150° - 150° = 60°. 因为点C为AD中点，所以AC = $\frac{1}{2}$AD = 2，所以AE = 2.

5思想方法分类讨论[2024浙江丽水期末,难]一副三角尺按如图所示的方式摆放在直线MN上(示意图),将三角尺ABP(含45°角的三角尺)绕点P以每秒15°的速度顺时针旋转，同时,三角尺PCD(含30°角的三角尺)也绕点P以每秒5°的速度逆时针旋转，当三角尺ABP的直角边PB与PN共线时停止旋转,同时,三角尺PCD 也停止旋转，设运动的时间为t s.

（1）用含t的代数式表示：∠NPD = ________；∠MPB = ________.
（2）当t为何值时,∠BPC = 5°？
（3）请从下列三个问题中选择一个完成作答.
①当t为何值时,PC与PB在一条直线上?
②当t为何值时,PC⊥PB?
③在旋转过程中是否存在这样的t值,使得射线PB是由射线PA、射线PC、射线PD中的其中两条组成的角的平分线？如果存在,请求出t的值;如果不存在,请说明理由.

答案：
【解】
(1)因为三角尺ABP是等腰直角三角形，且绕点P以每秒15°的速度顺时针旋转，所以∠MPB = (45 + 15t)°.
因为三角尺PCD是含30°角的直角三角形，且绕点P以每秒5°的速度逆时针旋转，所以∠NPD = (5t)°. 故答案为(5t)°，(45 + 15t)°.
(2)①两个三角尺碰到之前且∠BPC = 5°时，如图
(1)所示.
因为∠MPB = (45 + 15t)°，∠NPC = (30 + 5t)°，∠BPC = 5°，∠MPB + ∠NPC + ∠BPC = 180°，所以(45 + 15t)° + (30 + 5t)° + 5° = 180°，解得t = 5；

②两个三角尺碰到之后且∠BPC = 5°时，如图
(2)所示.
因为∠MPB = (45 + 15t)°，∠NPC = (30 + 5t)°，∠BPC = 5°，∠MPB + ∠NPC - ∠BPC = 180°，所以(45 + 15t)° + (30 + 5t)° - 5° = 180°，解得t = 5.5.
综上所述，当t为5或5.5时，∠BPC = 5°.
(3)(选择其中一个完成作答即可)
①当PC与PB在一条直线上时，如图
(3)所示.
因为∠MPB + ∠NPC = 180°，∠MPB = (45 + 15t)°，∠NPC = (30 + 5t)°，所以(45 + 15t)° + (30 + 5t)° = 180°，解得t = $\frac{21}{4}$，所以当t为$\frac{21}{4}$时，PC与PB在一条直线上.

②当PC⊥PB时，∠BPC = 90°.
ⅰ. 在两个三角尺碰到之前，如图
(4)所示，∠MPB + ∠NPC + ∠BPC = 180°，所以(45 + 15t)° + (30 + 5t)° + 90° = 180°，解得t = $\frac{3}{4}$；
ⅱ. 在两个三角尺碰到之后，∠MPB + ∠NPC - ∠BPC = 180°，所以(45 + 15t)° + (30 + 5t)° - 90° = 180°，解得t = $\frac{39}{4}$.
因为PB与PN共线时，三角尺停止旋转，此时∠MPB = 180°，所以(45 + 15t)° = 180°，解得t = 9，所以0 ≤ t ≤ 9，所以t = $\frac{39}{4}$不符合题意，舍去.
综上所述，当t为$\frac{3}{4}$时，PC⊥PB.
③存在.
ⅰ. 当射线PB是由射线PA、射线PC组成的角的平分线时，如图
(5)所示.
因为PB平分∠APC，所以∠APC = 2∠APB = 90°. 因为∠MPA + ∠APC + ∠NPC = 180°，∠MPA = (15t)°，∠NPC = (30 + 5t)°，所以(15t)° + 90° + (30 + 5t)° = 180°，解得t = 3；
关键点拨
(2)当∠BPC = 5°时，注意分两种情况讨论：①两个三角尺碰到之前；②两个三角尺碰到之后.
ⅱ. 当射线PB是由射线PA、射线PD组成的角的平分线时，如图
(6)所示.
因为PB平分∠APD，所以∠APD = 2∠APB = 90°. 因为∠MPA + ∠APD + ∠NPD = 180°，∠MPA = (15t)°，∠NPD = (5t)°，所以(15t)° + 90° + (5t)° = 180°，解得t = 4.5；
ⅲ. 当射线PB是由射线PC、射线PD组成的角的平分线时，如图
(7)所示.
因为PB平分∠CPD，所以∠BPD = $\frac{1}{2}$∠CPD = 15°.
因为∠MPB + ∠BPD + ∠NPD = 180°，∠MPB = (45 + 15t)°，∠NPD = (5t)°，所以(45 + 15t)° + 15° + (5t)° = 180°，解得t = 6.
综上所述，t的值为3或4.5或6.