《2025年初中必刷题七年级数学下册苏科版》

1[2024天津西青区期末]计算$(-3x)\left(-2x^{2}+\frac{2}{3}x - 4\right)$的结果是 （ ）
A. $-6x^{3}-2x^{2}+12x$
B. $6x^{3}-2x^{2}+12$
C. $6x^{3}+2x^{2}-12x$
D. $6x^{3}-2x^{2}+12x$

答案： 1. D 【解析】$(-3x)\left(-2x^{2}+\frac{2}{3}x - 4\right)=6x^{3}-2x^{2}+12x$。故选 D。
技巧总结：同且相同字母相同的两个单项式。
关键点拔：
(1)根据单项式乘多项式的运算法则进行计算。
(2)先根据单项式乘多项式进行计算，再合并。

2[2024湖北随州期末]在“单项式乘多项式”的课堂上，有这样一道题：$(x - 3y)\cdot(-6x)=x\cdot(-6x)\square(-3y)\cdot(-6x)$，“$\square$”内应填的符号为 （ ）
A. +
B. -
C. ×
D. ÷

答案：
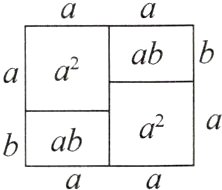
2. A 【解析】$(x - 3y)\cdot(-6x)=x\cdot(-6x)+(-3y)\cdot(-6x)$，所以“ ”内应填的符号为“$+$”。故选 A。

3通过计算几何图形的面积可表示一些代数恒等式，如图可表示的代数恒等式是 （ ）

A. $(a - b)^{2}=a^{2}-2ab + b^{2}$
B. $(a + b)^{2}=a^{2}+2ab + b^{2}$
C. $2a(a + b)=2a^{2}+2ab$
D. $(a + b)(a - b)=a^{2}-b^{2}$

答案： 3. C 【解析】大长方形的面积可以表示为$2a(a + b)$，也可以表示为四个小图形的面积之和，即$a^{2}+a^{2}+ab + ab=2a^{2}+2ab$，即$2a(a + b)=2a^{2}+2ab$。故选 C。

4[2024江苏淮安期中]计算$-2x^{2}\cdot(x^{2}+3x^{3}y - 4y^{2})$的结果中次数是6的项的系数是________.

答案： 4. -6 【解析】$-2x^{2}\cdot(x^{2}+3x^{3}y - 4y^{2})=-2x^{4}-6x^{5}y + 8x^{2}y^{2}$。因为$-6x^{5}y$的次数是 6，所以$-2x^{2}\cdot(x^{2}+3x^{3}y - 4y^{2})$的结果中次数是 6 的项的系数是 -6。故答案为 -6。

5[2024江苏扬州仪征质检]计算下列各题.
(1)$3a^{2}b(-4a^{2}b + 2ab^{2}-ab)$；
(2)$-5x\cdot(x^{2}y - xy^{2})-2x^{2}\left(\frac{1}{2}xy + y^{2}\right)$.

答案： 5. 【解】
(1)原式$=3a^{2}b\cdot(-4a^{2}b)+3a^{2}b\cdot2ab^{2}-3a^{2}b\cdot ab=-12a^{4}b^{2}+6a^{3}b^{3}-3a^{3}b^{2}$。
(2)原式$=-5x\cdot x^{2}y + 5x\cdot xy^{2}-2x^{2}\cdot\frac{1}{2}xy - 2x^{2}\cdot y^{2}=-5x^{3}y + 5x^{2}y^{2}-x^{3}y - 2x^{2}y^{2}=-6x^{3}y + 3x^{2}y^{2}$。

6[2024江苏镇江润州区质检]若$-x^{2}y = 2$，则$-xy(x^{5}y^{2}-x^{3}y + 2x)$的值为 （ ）
A. 16
B. 12
C. 8
D. 0

答案： 6. A 【解析】原式$=-x^{6}y^{3}+x^{4}y^{2}-2x^{2}y$，当$-x^{2}y = 2$时，$x^{2}y=-2$，所以原式$=-(x^{2}y)^{3}+(x^{2}y)^{2}-2x^{2}y=-(-2)^{3}+(-2)^{2}-2\times(-2)=16$。故选 A。

7如果$m^{2}-2m - 2 = 0$，那么代数式$3m(m - 2)+2$的值是______.

答案： 7. 8 【解析】当$m^{2}-2m - 2 = 0$时，$m^{2}-2m = 2$。原式$=3m^{2}-6m + 2 = 3(m^{2}-2m)+2 = 3\times2 + 2 = 6 + 2 = 8$。故答案为 8。

8计算：$2x(-x^{2}+3x - 4)+3x^{2}\left(\frac{1}{2}x + 1\right)$，其中$x = 1$.

答案： 8. 【解】原式$=-2x^{3}+6x^{2}-8x+\frac{3}{2}x^{3}+3x^{2}=-\frac{1}{2}x^{3}+9x^{2}-8x$。将$x = 1$代入，得原式$=\frac{1}{2}$。

9[2024江西吉安质检]为做好乡村振兴工作，上级决定在一块长方形空地上修建板房，作为扶贫事务所. 已知长方形空地长为$3a$，宽为$4ab - 2a$，则其面积为 （ ）
A. $12a^{2}b-6a^{2}$
B. $6a^{2}-12a^{2}b$
C. $6a^{2}b-12a^{2}$
D. $12a^{2}-6a^{2}b$

答案： 9. A 【解析】$3a\cdot(4ab - 2a)=12a^{2}b - 6a^{2}$，所以其面积为$12a^{2}b - 6a^{2}$。故选 A。

10[2024浙江温州期中]若要使$(x^{2}+ax + 5)\cdot(-6x^{3})+6x^{4}$的结果中不含$x^{4}$项，则常数$a$的值为________.

答案： 10. 1 【解析】$(x^{2}+ax + 5)\cdot(-6x^{3})+6x^{4}=-6x^{5}-6ax^{4}-30x^{3}+6x^{4}=-6x^{5}+(6 - 6a)x^{4}-30x^{3}$。因为$(x^{2}+ax + 5)\cdot(-6x^{3})+6x^{4}$的结果中不含$x^{4}$项，所以$6 - 6a = 0$，解得$a = 1$。故答案为 1。

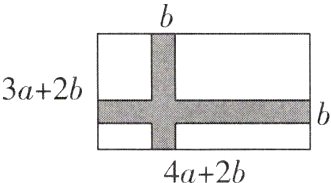
11[2023吉林长春双阳区期末]如图，为提高业主的宜居环境，某小区物业准备在一个长为$(4a + 2b)$米，宽为$(3a + 2b)$米的长方形草坪上修建两条宽为$b$米的小路，求小路的面积.（要求化成最简形式）

答案： 11. 【解】由题意得小路的面积为$b(3a + 2b)+b(4a + 2b)-b^{2}=3ab + 2b^{2}+4ab + 2b^{2}-b^{2}=(7ab + 3b^{2})$平方米。

12已知计算$(5 - 3x + mx^{2}-6x^{3})\cdot(-2x^{2})-x(-3x^{3}+nx - 1)$的结果中不含$x^{4}$和$x^{2}$的项，求$m$，$n$的值.

答案： 12. 【解】$(5 - 3x + mx^{2}-6x^{3})\cdot(-2x^{2})-x(-3x^{3}+nx - 1)=-10x^{2}+6x^{3}-2mx^{4}+12x^{5}+3x^{4}-nx^{2}+x=12x^{5}+(3 - 2m)x^{4}+6x^{3}+(-10 - n)x^{2}+x$，由结果中不含$x^{4}$和$x^{2}$的项，得$3 - 2m = 0$，$-10 - n = 0$，解得$m = 1.5$，$n=-10$。