《2025年初中必刷题七年级数学下册苏科版》

1. 已知四个数a,b,c,d,若a＞b,c=d,则　(　　)
A. a+c＞b+d
B. a+b＞c+d
C. a+c＞b−d
D. a+b＞c−d

答案： A　[解析]A选项，因为a＞b，c = d，所以a + c＞b + d，故该选项符合题意；B选项，当a = 2，b = 1，c = d = 3时，a + b＜c + d，故该选项不符合题意；C选项，当a = 2，b = 1，c = d = -3时，a + c＜b - d，故该选项不符合题意；D选项，当a = -1，b = -2，c = d = 3时，a + b＜c - d，故该选项不符合题意。故选A。

2. [2024福建泉州质检]若x＞y,则x−3________y−3.

答案： [解析]因为x＞y，所以x - 3＞y - 3。故答案为x - 3＞y - 3。

3. [2024浙江杭州期末]已知a＞b,则一定有−4a□−4b,“□”中应填的符号是　(　　)
A. ＞
B. ＜
C. ≥
D. =

答案： B　[解析]将不等式a＞b两边同乘 -4，不等号的方向改变，所以 -4a＜ -4b，所以“口”中应填的符号是“＜”。故选B。

4. [2024江苏南通期中]若x＞y,则下列不等式中一定成立的是　(　　)
A. x²＞y²
B. −3x＞−3y
C. $\frac{x}{2}$____$\frac{y}{2}$
D. 1−x＜1−y

答案： [解析]A. x²，y²的大小无法确定，故本选项错误；B. -3x＜ -3y，故本选项错误；C. $\frac{x}{2}$＞$\frac{y}{2}$，故本选项错误；D. 1 - x＜1 - y，故本选项正确。

5. [2023江苏苏州姑苏区质检]若−$\frac{a}{3}$＜−$\frac{b}{9}$,则3a________b.(填“＜”“＞”或“=”)

答案： ＞　[解析]因为 -$\frac{a}{3}$＜ -$\frac{b}{9}$，所以 -3a＜ -b，所以3a＞b。故答案为＞。

6. [2024陕西西安质检]若a＜b,则(k²+1)a ________(k²+1)b.

答案： ＜　[解析]因为a＜b，且k² + 1＞0，所以(k² + 1)a＜(k² + 1)b。故答案为＜。

7. 已知x＞y.
(1)比较3−x与3−y的大小;
(2)若3+ax＞3+ay,求a的取值范围.

答案： [解]
(1)因为x＞y，所以 -x＜ -y，所以3 - x＜3 - y。
(2)因为x＞y，3 + ax＞3 + ay，所以a＞0。

8. [2024江苏宿迁期末]已知关于x的不等式(1−a)x＞2中x的取值范围为x＜$\frac{2}{1−a}$,求a的取值范围.

答案： [解]因为关于x的不等式(1 - a)x＞2中x的取值范围为x＜$\frac{2}{1 - a}$，所以不等式(1 - a)x＞2在两边同时除以(1 - a)后不等号的方向发生改变，所以1 - a＜0，所以1 - a + a＜a，所以a＞1。

9. [2024江苏连云港质检]根据不等式的基本性质,请将下列不等式化为“x＞a”或“x＜a”的形式.
(1)x−4＞3;
(2)2x−3＜x−2;
(3)$\frac{1}{2}x + 1$＞−3;
(4)−2x−4＜4x+4.

答案： [解]
(1)因为x - 4＞3，所以x - 4 + 4＞3 + 4，所以x＞7。
(2)因为2x - 3＜x - 2，所以2x - 3 + (-x + 3)＜x - 2 + (-x + 3)，所以x＜1。
(3)因为$\frac{1}{2}$x + 1＞ -3，所以2×($\frac{1}{2}$x + 1)＞ -3×2，所以x + 2＞ -6，所以x + 2 - 2＞ -6 - 2，所以x＞ -8。
(4)因为 -2x - 4＜4x + 4，所以 -2x - 4 + (4 - 4x)＜4x + 4 + (4 - 4x)，所以 -6x＜8，所以 -$\frac{1}{6}$×(-6x)＞ -$\frac{1}{6}$×8，所以x＞ -$\frac{4}{3}$。

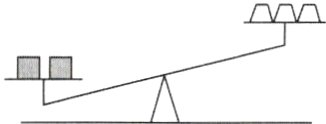
10. 如图,一个倾斜的天平两边分别放有小立方体和砝码,每个砝码的质量都是5克,每个小立方体的质量都是m克,则m的取值范围为________.

答案： m＞$\frac{15}{2}$　[解析]由题意得2m＞3×5，所以m＞$\frac{15}{2}$。故答案为m＞$\frac{15}{2}$。

11. 苹果的进价是每千克5.7元,销售中估计有5%的苹果正常损耗,则售价x(元/千克)满足________时，可避免亏本.

答案： x≥6　[解析]由题意可得x(1 - 5%)≥5.7，所以x≥6。

12. 小明说a＞2a永远不可能成立,因为不等式两边都除以a,得到1＞2这个错误结论,小明的说法正确吗？请说明理由.

答案： [解]小明的说法不正确。理由如下：小明默认a＞0，未对a的取值范围进行分类讨论。当a＞0时，由1＜2得a＜2a；当a = 0时，a = 2a；当a＜0时，由1＜2得a＞2a。综上，当a＜0时，a＞2a成立。故小明的说法不正确。