《2025年初中必刷题七年级数学下册苏科版》

一、选择题（本大题共6小题，每小题4分，共24分）

答案：

1[2024江苏南京模拟]计算$(-2a^{2})^{3}$的结果是 （ ）
A. $6a^{6}$
B. $-6a^{6}$
C. $8a^{6}$
D. $-8a^{6}$

答案： 1. D 【解析】$(-2a^{2})^{3}=(-2)^{3}(a^{2})^{3}=-8a^{6}$. 故选 D.

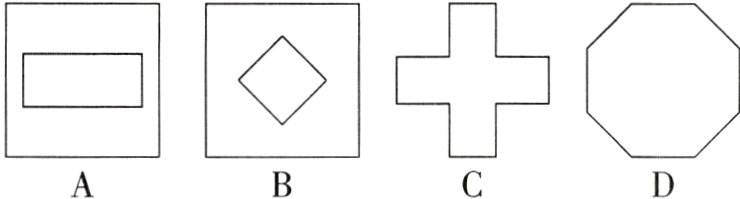
2[2024山东青岛质检]如图，把一个正方形对折两次后沿虚线剪下一个小角，展开后得到的图形是 （ ）

答案： 2. B 【解析】由题意得，展开后得到的图形是原正方形中间缺了一个四条边均相等的小四边形. 故选 B.

3[2024江苏苏州期末]某公司计划开发3 nm级制程芯片. 其中，$3\ nm = 0.000\ 000\ 003\ m$，数据$0.000\ 000\ 003$用科学记数法可以表示为 （ ）
A. $0.3\times10^{-8}$
B. $3\times10^{-9}$
C. $3\times10^{-10}$
D. $30\times10^{-10}$

答案： 3. B 【解析】$0.000000003 = 3×10^{-9}$. 故选 B.

4[2024江苏南京期中]观察等式$(2a - 1)^{a + 2}=1$，其中a的值是 （ ）
A. -2
B. 1或-2
C. 0或1
D. 1或-2或0

答案： 4. D 【解析】情况一：指数为 0，底数不为 0，即$a + 2 = 0$，$2a - 1≠0$，解得$a = -2$；情况二：底数为 1，指数为任意数，即$2a - 1 = 1$，解得$a = 1$；情况三：底数为 -1，指数为偶数，即$2a - 1 = -1$，解得$a = 0$，代入$a + 2$得$a + 2 = 2$，为偶数，成立. 综上，$a$的值是 1 或 -2 或 0. 故选 D.

5[2024江苏镇江质检]设m，n是正整数，且m＞n，若$9^{m}$与$9^{n}$的末尾两位数字相同，则$m - n$的最小值为 （ ）
A. 9
B. 10
C. 11
D. 12

答案： 5. B 【解析】由题意知，$9^{m}-9^{n}=9^{n}(9^{m - n}-1)$是 100 的倍数. 因为$9^{n}$与 100 互质，所以$9^{m - n}-1$是 100 的倍数，所以$9^{m - n}$的末尾两位数字是 01，所以$m - n$的数值一定是偶数. 设$m - n = 2t$（$t$为正整数），则$9^{m - n}=9^{2t}=(9^{2})^{t}=81^{t}$. 因为$81^{2}$的末尾两位数字为 61，$81^{3}$的末尾两位数字为 41，$81^{4}$的末尾两位数字为 21，$81^{5}$的末尾两位数字为 01，所以$t$的最小值为 5，所以$m - n$的最小值为 10. 故选 B.

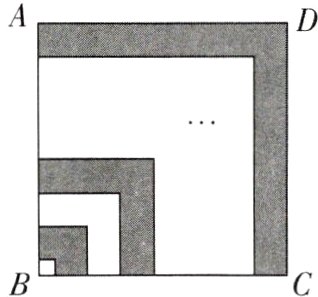
6[2024江苏扬州期末]如果一个正整数能表示为两个连续奇数的平方差，那么称这个正整数为“奇特数”. 例如：$8 = 3^{2}-1^{2}$，$16 = 5^{2}-3^{2}$，$24 = 7^{2}-5^{2}$，则8，16，24这三个数都是“奇特数”. 如图所示，拼叠的正方形边长是从1开始的连续奇数，…，按此规律拼叠到正方形ABCD，其边长为203，则阴影部分的面积为 （ ）

A. 19 208
B. 20 000
C. 20 706
D. 20 808

答案： 6. D 【解析】阴影部分的面积为$3^{2}-1^{2}+7^{2}-5^{2}+11^{2}-9^{2}+\cdots+203^{2}-201^{2}=(3^{2}-1^{2})+(7^{2}-5^{2})+(11^{2}-9^{2})+\cdots+(203^{2}-201^{2})=(3 - 1)(3 + 1)+(7 - 5)(7 + 5)+(11 - 9)(11 + 9)+\cdots+(203 - 201)(203 + 201)=2×(1 + 3 + 5 + 7 + 9 + 11+\cdots+201 + 203)=2×\frac{(1 + 203)×102}{2}=20808$. 故选 D.

二、填空题（本大题共6小题，每小题4分，共24分）

答案：

7[2024江苏泰州质检]如图，已知四边形ABCD与四边形EFGH关于直线BD上某个点成中心对称，则点B的对应点是点________.

答案：
7. H 【解析】如图，连接$AG$，交直线$BD$于点$O$. 由题意知，点$O$为对称中心，则点$B$的对应点是点$H$. 故答案为$H$.

期中综合测试即7易错警示注意要分指数为 0，底数不为 0；底数为 1，指数为任意数；底数为 -1，指数为偶数三种情况讨论.本题的解题关键是抓住每一块阴影部分的面积都是两个连续奇数的平方差，利用平方差公式简便运算求解.

8[2024江苏南京期中]若一个长方体的长、宽、高分别是$3x - 4$，$x + 2$和$2x$，则它的体积是________.

答案： 8. $6x^{3}+4x^{2}-16x$ 【解析】$2x(3x - 4)(x + 2)=(6x^{2}-8x)(x + 2)=6x^{3}+4x^{2}-16x$. 故答案为$6x^{3}+4x^{2}-16x$.

9[2024江苏南通期末]若$x^{2}-6x + 1 = 0$，则$x^{2}+\frac{1}{x^{2}}=$________.

答案： 9. 34 【解析】因为$x^{2}-6x + 1 = 0$，所以$x≠0$，所以方程$x^{2}-6x + 1 = 0$两边同时除以$x$，得$x - 6+\frac{1}{x}=0$，所以$x+\frac{1}{x}=6$，则$x^{2}+\frac{1}{x^{2}}=(x+\frac{1}{x})^{2}-2=36 - 2 = 34$. 故答案为 34.

10[2024江苏无锡期中]如图，$\triangle APT$与$\triangle CPT$关于直线PT对称，$\angle A=\angle APT$，延长AT交PC于点F，当$\angle A=$________°时，$\angle FTC=\angle C$.

答案： 10. 36 【解析】因为$\triangle APT$与$\triangle CPT$关于直线$PT$对称，所以$\angle A=\angle C$，$TA = TC$，$\angle APT=\angle CPT$. 因为$\angle A=\angle APT$，所以$\angle A=\angle C=\angle APT=\angle CPT$. 因为$\angle FTC=\angle C$，所以$\angle AFP = 180^{\circ}-\angle AFC=\angle C+\angle FTC = 2\angle C = 2\angle A$. 因为$\angle A+\angle APF+\angle AFP = 180^{\circ}$，所以$5\angle A = 180^{\circ}$，所以$\angle A = 36^{\circ}$. 故答案为 36.

11[2024江苏镇江调研]现有若干张卡片，分别写有1，-2，4，-8，16，-32，…，小明从中随机取出三张卡片，要满足三张卡片上的数字乘积为$2^{100}$，其中三数之和的最大值记为A，最小值记为B，则$A + B - 4$等于________.

答案： 11. $-2^{98}$ 【解析】由题意知，卡片上的数字依次为$(-2)^{0}$，$(-2)^{1}$，$(-2)^{2}$，$(-2)^{3}$，$(-2)^{4}$，$(-2)^{5}$，$\cdots$. 因为三张卡片上的数字乘积为$2^{100}$，所以使三数之和最大的三个数为$(-2)^{0}$，$(-2)^{2}$，$(-2)^{98}$，使三数之和最小的三个数为$(-2)^{0}$，$(-2)^{1}$，$(-2)^{99}$，所以$A = (-2)^{0}+(-2)^{2}+(-2)^{98}$，$B = (-2)^{0}+(-2)^{1}+(-2)^{99}$，所以$A + B - 4 = (-2)^{0}+(-2)^{2}+(-2)^{98}+(-2)^{0}+(-2)^{1}+(-2)^{99}-4 = 1 + 4 + 2^{98}+1 - 2 - 2^{99}-4 = 2^{98}-2^{99}=2^{98}(1 - 2)=-2^{98}$. 故答案为$-2^{98}$.

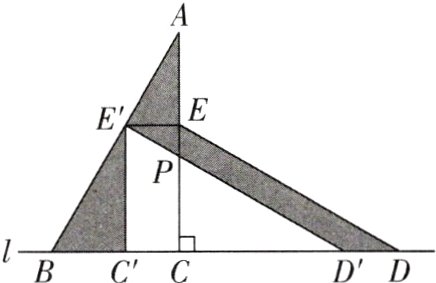
12[2024吉林长春质检]如图，直线l上有形状和大小相同的$\triangle ABC$和$\triangle DEC$，$\angle ACB=\angle DCE = 90^{\circ}$，$\angle BAC=\angle EDC = 30^{\circ}$，将$\triangle DEC$沿直线l向左平移得到$\triangle D'E'C'$，点$E'$落在AB上，$E'D'$与AC交于点P. 给出下面四个结论：
①$\angle CPD' = 60^{\circ}$；②$AB\perp E'D'$；③$\triangle PEE'$和$\triangle PCD'$的周长之和等于$\triangle ABC$的周长；④图中阴影部分的面积之和大于$\triangle ABC$的面积.
其中所有正确结论的序号是________.

答案： 12. ①②③ 【解析】由题意得$AB = DE$，$BC = CE$，$AC = CD$，$\angle ABC=\angle CED = 60^{\circ}$，$DE// D'E'$，$DE = D'E'$，$EE' = DD'$. ①因为$DE// D'E'$，所以$\angle CPD'=\angle CED = 60^{\circ}$，故①正确；②因为$\angle CD'E'=\angle EDC = 30^{\circ}$，$\angle ABC = 60^{\circ}$，所以$\angle D'E'B = 180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}$，所以$D'E'\perp AB$，故②正确；③因为$\triangle PEE'$和$\triangle PCD'$的周长之和为$PE + PE'+EE'+PC + PD'+CD' = CE + CD + DE$，即与$\triangle CDE$的周长相等，而$\triangle ABC$与$\triangle CDE$形状、大小完全一样，所以$\triangle PEE'$和$\triangle PCD'$的周长之和等于$\triangle ABC$的周长，故③正确；④易知$S_{平行四边形DD'E'E}=S_{长方形CC'E'E}$，所以$S_{阴影部分}=S_{\triangle ABC}$，故④不正确. 综上所述，正确的结论有①②③. 故答案为①②③.