《2025年初中必刷题七年级数学下册苏科版》

1[2024上海青浦区期末]关于代数式$(a + 1)^{0}$，下列说法正确的是 （ ）
A. $(a + 1)^{0}$的值一定是0
B. $(a + 1)^{0}$的值一定是1
C. 当$a\neq 0$时，$(a + 1)^{0}$的值是1
D. 当$a\neq - 1$时，$(a + 1)^{0}$的值是1

答案： D【解析】$(a + 1)^{0}$有意义的条件是$a + 1\neq0$，解得$a\neq - 1$，即当$a\neq - 1$时，$(a + 1)^{0}=1$. 故选 D.

2[2024江苏徐州质检]若$a = - 0.2^{2}$，$b = - 2^{-2}$，$c = (-\frac{1}{4})^{-2}$，$d = (-\frac{1}{4})^{0}$，则$a$，$b$，$c$，$d$的大小关系是 （ ）
A. $a\lt b\lt c\lt d$
B. $b\lt a\lt d\lt c$
C. $a\lt d\lt c\lt b$
D. $c\lt a\lt d\lt b$

答案： B【解析】因为$a=-0.2^{2}=-\frac{1}{25}$，$b=-2^{-2}=-\frac{1}{4}$，$c=(-\frac{1}{4})^{-2}=16$，$d=(-\frac{1}{4})^{0}=1$，且$-\frac{1}{4}＜-\frac{1}{25}＜1＜16$，所以$b ＜ a ＜ d ＜ c$. 故选 B.

3[2024浙江金华期末]若等式$(x - 3)^{x + 1}=1$成立，则使等式成立的$x$的值的个数为 （ ）
A. 2
B. 3
C. 4
D. 5

答案： A【解析】根据任何不等于 0 的数的 0 次幂都等于 1，可得$x + 1 = 0$，解得$x = - 1$，当$x = - 1$时，$x - 3\neq0$，因此$x = - 1$符合题意；由 1 的任何次幂都等于 1，可得$x - 3 = 1$，解得$x = 4$；由 - 1 的偶数次幂等于 1，可得$x - 3 = - 1$，解得$x = 2$，当$x = 2$时，$x + 1 = 3$不是偶数，因此$x = 2$不符合题意. 综上所述，$x = - 1$或$x = 4$，共 2 个. 故选 A.

4[2023福建宁德蕉城区期中]已知$a$，$b$，$c$为自然数，且满足$2^{a}\times 3^{b}\times 4^{c}=192$，则$a + b - c$的值可能是 （ ）
A. -2
B. 1
C. 2
D. 4

答案： C【解析】因为$2^{a}\times3^{b}\times4^{c}=2^{a}\times3^{b}\times(2^{2})^{c}=2^{a + 2c}\cdot3^{b}=2^{6}\cdot3$，所以$a + 2c = 6$，$b = 1$. 因为$a$，$b$，$c$为自然数，所以当$c = 0$时，$a = 6$，则$a + b - c = 7$；当$c = 1$时，$a = 4$，则$a + b - c = 4$；当$c = 2$时，$a = 2$，则$a + b - c = 1$；当$c = 3$时，$a = 0$，则$a + b - c = - 2$，所以$a + b - c$的值不可能为 2. 故选 C.

5[2024四川广元二模]纳米（Nanometer，符号：nm）是长度单位，1纳米$ = 10^{-9}$米. 已知一根头发的直径约为50 000纳米，用科学记数法应表示为_______米.

答案： $5\times10^{-5}$【解析】50000 纳米$=0.00005$米$=5\times10^{-5}$米. 故答案为$5\times10^{-5}$.

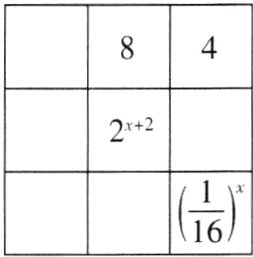
6[2024福建福州期末]在一个数学九宫格中，当处于同一横行，同一竖行，同一斜对角线上的3个数之积都相等时称之为“积的九宫归位”. 在如图所示的九宫格中，已填写了一些数或式子，为了完成“积的九宫归位”，则$x$的值为_______.

答案： - 1【解析】由题意可得，$2^{x + 2}\cdot(\frac{1}{16})^{x}=4\times8$，所以$2^{x + 2}\cdot2^{-4x}=2^{5}$，即$2^{2 - 3x}=2^{5}$，所以$2 - 3x = 5$，所以$3x = - 3$，解得$x = - 1$. 故答案为 - 1.

7新考法[2023江苏连云港期末]定义一种新运算：$\int_{b}^{a}nx^{n - 1}dx=a^{n}-b^{n}$，例如$\int_{m}^{k}2xdx=k^{2}-m^{2}$. 若$\int_{2}^{k}(-x^{-2})dx=-1$，则$k =$_______.

答案： - 2【解析】由题意得，$\int_{2}^{k}(-x^{-2})dx=k^{-1}-2^{-1}=\frac{1}{k}-\frac{1}{2}=-1$，解得$k = - 2$. 故答案为 - 2.

8[2023江苏南京栖霞区期末]已知$k^{a}=4$，$k^{b}=6$，$k^{c}=9$，$2^{b + c}\cdot 3^{b + c}=6^{a - 2}$，则$9^{a}\div 27^{b}=$_______.

答案： 9【解析】$9^{a}\div27^{b}=(3^{2})^{a}\div(3^{3})^{b}=(3)^{2a - 3b}$. 因为$k^{a}=4$，$k^{b}=6$，$k^{c}=9$，所以$k^{a}\cdot k^{c}=k^{b}\cdot k^{b}$，所以$k^{a + c}=k^{2b}$，所以$a + c = 2b$，所以$c = 2b - a$. 因为$2^{b + c}\cdot3^{b + c}=6^{a - 2}$，所以$(2\times3)^{b + c}=6^{a - 2}$，所以$b + c = a - 2$，所以$c = a - 2 - b$，所以$2b - a = a - 2 - b$，所以$2a - 3b = 2$，所以$9^{a}\div27^{b}=(3)^{2a - 3b}=3^{2}=9$. 故答案为 9.

9[2023江苏苏州姑苏区质检]计算：
（1）$-2^{2}+(\pi - 3)^{0}+(\frac{1}{2})^{-2}$；
（2）$(m - 1)^{3}(1 - m)^{4}+(1 - m)^{7}$.

答案： 【解】
(1)原式$=-4 + 1 + 4 = 1$.
(2)原式$=-(1 - m)^{3}(1 - m)^{4}+(1 - m)^{7}=-(1 - m)^{7}+(1 - m)^{7}=0$.

10[2024江苏扬州质检]幂的运算性质在一定条件下具有可逆性，若$(ab)^{m}=a^{m}b^{m}$，则$a^{m}b^{m}=(ab)^{m}$（$m$为正整数）. 请运用所学知识解答下列问题：
（1）已知$2^{x + 3}\cdot 3^{x + 3}=36^{x - 2}$，求$x$的值.
（2）已知$3\times 2^{x + 3}\times 4^{x + 3}=96$，求$x$的值.

答案： 【解】
(1)因为$2^{x + 3}\cdot3^{x + 3}=36^{x - 2}$，所以$(2\times3)^{x + 3}=(6^{2})^{x - 2}$，即$6^{x + 3}=6^{2(x - 2)}$，所以$x + 3 = 2(x - 2)$，解得$x = 7$.

11[2024江苏盐城期中]如果$x^{n}=y$，那么我们规定$[x,y]=n$. 例如：因为$3^{2}=9$，所以$[3,9]=2$.
（1）$[-3,81]=$_______；若$[2,y]=6$，则$y =$_______.
（2）已知$[3,60]=a$，$[3,4]=b$，$[3,m]=c$，若$a - b = c$，则$m =$_______.
（3）已知$[4,28]=x$，$[7,28]=y$，令$t=\frac{x + y}{2xy}$.
①求$\frac{49^{y}}{64^{x}}$的值；
②求$t$的值.

答案：