第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
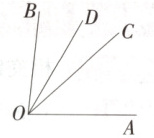
例 3 如图,$ OC $ 是 $ \angle AOB $ 的平分线,$ OD $ 是 $ \angle COB $ 的平分线,$ \angle AOD=60^{\circ} $,则 $ \angle AOB= $
80
$ ^{\circ} $.
答案:
例3 80
练 1 [25·广安] 若 $ \angle A=25^{\circ} $,则 $ \angle A $ 的余角为 (
A.$ 25^{\circ} $
B.$ 65^{\circ} $
C.$ 75^{\circ} $
D.$ 155^{\circ} $
B
)A.$ 25^{\circ} $
B.$ 65^{\circ} $
C.$ 75^{\circ} $
D.$ 155^{\circ} $
答案:
练1 B
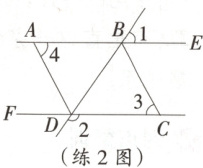
练 2 [优质原创] 如图,直线 $ BD $ 分别交 $ AE,CF $ 于点 $ B,D $,连接 $ AD,BC $,若 $ DA $ 平分 $ \angle BDF $,$ \angle 3= \angle 4 $,若 $ \angle 1=50^{\circ} $,$ \angle 2= 130^{\circ} $,则 $ \angle CBD $ 的度数为 (
A.$ 45^{\circ} $
B.$ 50^{\circ} $
C.$ 60^{\circ} $
D.$ 65^{\circ} $
D
)
A.$ 45^{\circ} $
B.$ 50^{\circ} $
C.$ 60^{\circ} $
D.$ 65^{\circ} $
答案:
练2 D
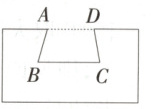
例 4 [25·河北 2 题] 榫卯结构是两个构件采取凹凸结合的连接方式.如图是某个构件的截面图,其中 $ AD// BC $,$ \angle ABC=70^{\circ} $,则 $ \angle BAD=($
A.$ 70^{\circ} $
B.$ 100^{\circ} $
C.$ 110^{\circ} $
D.$ 130^{\circ} $
C
$) $
A.$ 70^{\circ} $
B.$ 100^{\circ} $
C.$ 110^{\circ} $
D.$ 130^{\circ} $
答案:
例4 C
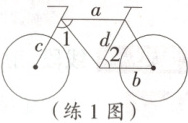
练 1 [25·石家庄 18 县区一模] 如图是一辆竖直放在地面上的自行车的示意图,其中 $ a// b $,$ c// d $,$ \angle 1=115^{\circ} $,则 $ \angle 2=($
A.$ 55^{\circ} $
B.$ 60^{\circ} $
C.$ 65^{\circ} $
D.$ 70^{\circ} $
C
$) $
A.$ 55^{\circ} $
B.$ 60^{\circ} $
C.$ 65^{\circ} $
D.$ 70^{\circ} $
答案:
练1 C
练 2 [25·深圳] 如图为小颖在试鞋镜前的光路图,入射光线 $ OA $ 经平面镜后反射入眼,若 $ CB// OA $,$ \angle CBO=122^{\circ} $,$ \angle BON=90^{\circ} $,则入射角 $ \angle AON $ 的度数为 (
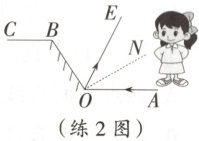
A.$ 22^{\circ} $
B.$ 32^{\circ} $
C.$ 35^{\circ} $
D.$ 122^{\circ} $
B
)
A.$ 22^{\circ} $
B.$ 32^{\circ} $
C.$ 35^{\circ} $
D.$ 122^{\circ} $
答案:
练2 B
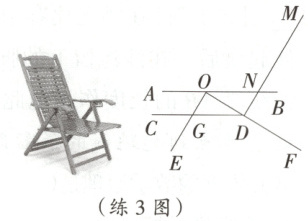
练 3 如图是一种躺椅及其简化结构示意图,扶手 $ AB $ 与底座 $ CD $ 都平行于地面 $ EF $,前支架 $ OE $ 与后支架 $ OF $ 分别与 $ CD $ 交于点 $ G $ 和点 $ D $,$ AB $ 与 $ DM $ 交于点 $ N $,$ \angle AOE=\angle BNM $.
(1)求证:$ OE// DM $;
(2)若 $ OE $ 平分 $ \angle AOF $,$ \angle ODC=30^{\circ} $,求扶手 $ AB $ 与靠背 $ DM $ 的夹角 $ \angle ANM $ 的度数.
(1)求证:$ OE// DM $;
(2)若 $ OE $ 平分 $ \angle AOF $,$ \angle ODC=30^{\circ} $,求扶手 $ AB $ 与靠背 $ DM $ 的夹角 $ \angle ANM $ 的度数.

答案:
练3 解:
(1)证明:$\because \angle BNM = \angle AND$,
$\angle AOE = \angle BNM$,$\therefore \angle AOE = \angle AND$,
$\therefore OE // DM$;
(2)$\because AB$与底座$CD$都平行于地面
$EF$,$\therefore AB // CD$,$\therefore \angle BOD = \angle ODC = 30^{\circ}$,
$\because \angle AOF + \angle BOD = 180^{\circ}$,
$\therefore \angle AOF = 150^{\circ}$.
$\because OE$平分$\angle AOF$,
$\therefore \angle EOF = \frac{1}{2} \angle AOF = 75^{\circ}$,
$\therefore \angle BOE = \angle BOD + \angle EOF = 105^{\circ}$,
$\because OE // DM$,
$\therefore \angle ANM = \angle BOE = 105^{\circ}$.
(1)证明:$\because \angle BNM = \angle AND$,
$\angle AOE = \angle BNM$,$\therefore \angle AOE = \angle AND$,
$\therefore OE // DM$;
(2)$\because AB$与底座$CD$都平行于地面
$EF$,$\therefore AB // CD$,$\therefore \angle BOD = \angle ODC = 30^{\circ}$,
$\because \angle AOF + \angle BOD = 180^{\circ}$,
$\therefore \angle AOF = 150^{\circ}$.
$\because OE$平分$\angle AOF$,
$\therefore \angle EOF = \frac{1}{2} \angle AOF = 75^{\circ}$,
$\therefore \angle BOE = \angle BOD + \angle EOF = 105^{\circ}$,
$\because OE // DM$,
$\therefore \angle ANM = \angle BOE = 105^{\circ}$.
查看更多完整答案,请扫码查看


