第143页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
1. 【项目式学习】制作“E”形视力表.
【课题实施】根据标准对数视力表(测试距离为5m),以小组合作方式,制作变更测试距离的视力表.
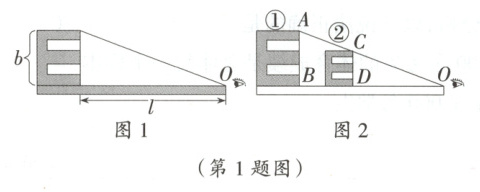
【课题结论】(1)如图1,利用“E”的高度b与它到眼睛的水平距离l之比(即$\dfrac{b}{l}$)来刻画视力.(2)大小不同的“E”,只要它们这一比值(即$\dfrac{b}{l}$)相同,那么用它们测得的视力就相同.
【课题应用】问题1:根据图2所示,水平桌面上依次放着①号和②号大小不一样的两个“E”字,将②号“E”字沿水平桌面向右移动,直至从观测点O看去,对应顶点A,C,O在同一直线上为止,其中AB是①号“E”字的高度,CD是②号“E”字的高度,请用所学知识证明:此时①号“E”字与②号“E”字测试的视力相同;
问题2:小明想制作一张测试距离为3m的“E”形视力表.如图2所示,①号“E”字是标准对数视力表中视力为4.2的“E”字,其高度AB为45mm,求小明在制作视力为4.2的②号“E”字时,②号“E”字的高度CD应为多少毫米?(A,C,O在一条直线上,B,D,O在一条直线上)
【课题实施】根据标准对数视力表(测试距离为5m),以小组合作方式,制作变更测试距离的视力表.
【课题结论】(1)如图1,利用“E”的高度b与它到眼睛的水平距离l之比(即$\dfrac{b}{l}$)来刻画视力.(2)大小不同的“E”,只要它们这一比值(即$\dfrac{b}{l}$)相同,那么用它们测得的视力就相同.
【课题应用】问题1:根据图2所示,水平桌面上依次放着①号和②号大小不一样的两个“E”字,将②号“E”字沿水平桌面向右移动,直至从观测点O看去,对应顶点A,C,O在同一直线上为止,其中AB是①号“E”字的高度,CD是②号“E”字的高度,请用所学知识证明:此时①号“E”字与②号“E”字测试的视力相同;
问题2:小明想制作一张测试距离为3m的“E”形视力表.如图2所示,①号“E”字是标准对数视力表中视力为4.2的“E”字,其高度AB为45mm,求小明在制作视力为4.2的②号“E”字时,②号“E”字的高度CD应为多少毫米?(A,C,O在一条直线上,B,D,O在一条直线上)

答案:
1. 解:问题1:证明:由题可得AB//CD,
∴∠ABO = ∠CDO,∠BAO = ∠DCO,
∴△ABO∽△CDO,
∴$\frac{CD}{AB} = \frac{OD}{OB}$,
∴$\frac{CD}{OD} = \frac{AB}{OB} = \frac{b}{l}$,
∴①号“E”字与②号“E”字测试的视力相同;
问题2:由
(1)可得,$\frac{CD}{OD} = \frac{AB}{OB}$,
∵AB = 45mm,OB = 5m = 5000mm,
OD = 3m = 3000mm,
∴$\frac{CD}{3000} = \frac{45}{5000}$,
∴CD = 27mm.
答:②号“E”字的高度CD应为27mm.
∴∠ABO = ∠CDO,∠BAO = ∠DCO,
∴△ABO∽△CDO,
∴$\frac{CD}{AB} = \frac{OD}{OB}$,
∴$\frac{CD}{OD} = \frac{AB}{OB} = \frac{b}{l}$,
∴①号“E”字与②号“E”字测试的视力相同;
问题2:由
(1)可得,$\frac{CD}{OD} = \frac{AB}{OB}$,
∵AB = 45mm,OB = 5m = 5000mm,
OD = 3m = 3000mm,
∴$\frac{CD}{3000} = \frac{45}{5000}$,
∴CD = 27mm.
答:②号“E”字的高度CD应为27mm.
2. 综合与实践
【定义】在$\triangle ABC$中,P是边AC上一点,若$AB^{2}=AP· AC$,则称点P是边AC关于边AB的“白银点”.
【概念理解】
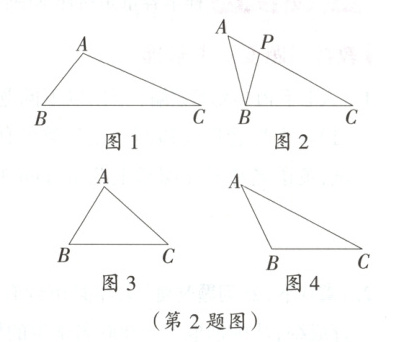
(1)如图1,请利用尺规作图在$\triangle ABC$中作出边AC关于边AB的“白银点”P;(不要求写作法,保留作图痕迹)
【性质应用】
(2)如图2,在$\triangle ABC$中,若$AB = 4$,$BC = 6$,$AC = 8$,点P是边AC关于边AB的“白银点”,请求出BP的值;
【拓展提升】
(3)①如图3,在$\triangle ABC$中,若$AB = 4$,$BC = 6$,$\angle A = 2\angle C$,请求出AC的值;
②如图4,在$\triangle ABC$中,若$AB = 4$,$AC = 8$,$\angle C = 45^{\circ}-\dfrac{1}{2}\angle A$,请求出BC的值.
【定义】在$\triangle ABC$中,P是边AC上一点,若$AB^{2}=AP· AC$,则称点P是边AC关于边AB的“白银点”.
【概念理解】
(1)如图1,请利用尺规作图在$\triangle ABC$中作出边AC关于边AB的“白银点”P;(不要求写作法,保留作图痕迹)
【性质应用】
(2)如图2,在$\triangle ABC$中,若$AB = 4$,$BC = 6$,$AC = 8$,点P是边AC关于边AB的“白银点”,请求出BP的值;
【拓展提升】
(3)①如图3,在$\triangle ABC$中,若$AB = 4$,$BC = 6$,$\angle A = 2\angle C$,请求出AC的值;
②如图4,在$\triangle ABC$中,若$AB = 4$,$AC = 8$,$\angle C = 45^{\circ}-\dfrac{1}{2}\angle A$,请求出BC的值.

答案:
2. 解:
(1)如图1,点P即为所作;

(2)
∵点P是边AC关于边AB的“白银点”,
∴$AB^{2} = AP·AC$,
即$\frac{AP}{AB} = \frac{AB}{AC}$,又
∵∠A = ∠A,
∴△ABP∽△ACB,
∴$\frac{BP}{BC} = \frac{AB}{AC}$,
又
∵AB = 4,AC = 8,BC = 6,
∴$\frac{BP}{6} = \frac{4}{8}$,
∴BP = 3;
(3)①如图2,作∠BAC的平分线AD交BC于点D,

∴∠BAD = ∠CAD = $\frac{1}{2}$∠BAC,
又
∵∠BAC = 2∠C,
∴∠C = ∠CAD,
∴AD = CD,
∵∠ADB = ∠C + ∠CAD = 2∠C,
∴∠ADB = ∠BAC,
又
∵∠B = ∠B,
∴△BDA∽△BAC,
∴$\frac{BD}{BA} = \frac{BA}{BC} = \frac{AD}{AC}$,
∵AB = 4,BC = 6,
∴$BD = \frac{AB^{2}}{BC} = \frac{16}{6} = \frac{8}{3}$,
∴AD = CD = BC - BD = 6 - $\frac{8}{3} = \frac{10}{3}$,
∴$AC = \frac{AB×AD}{BD} = \frac{4×\frac{10}{3}}{\frac{8}{3}} = 5$;
②如图3,过点B作BD⊥AC于点D,

∴∠A + ∠ABD = 90°,
∵∠C = 45° - $\frac{1}{2}$∠A,
∴90° - ∠A = 2∠C,
∴∠ABD = 2∠C,
作∠ABD的平分线交AC于点E,
∴∠ABE = ∠DBE = $\frac{1}{2}$∠ABD,
∴∠ABE = ∠DBE = ∠C,
又
∵∠A = ∠A,
∴△ABE∽△ACB,
∴$\frac{AB}{AC} = \frac{AE}{AB} = \frac{BE}{BC}$,又
∵AB = 4,AC = 8,
∴AE = 2,CE = AC - AE = 8 - 2 = 6,$\frac{BE}{BC} = \frac{1}{2}$,
∴$BE = \frac{1}{2}BC$,又
∵∠C + ∠DBC = 90°,
∠DBE = ∠C,
∴∠DBE + ∠DBC = ∠DBC + ∠C = 90°,
∴BE⊥BC,
∴$BC^{2} + BE^{2} = CE^{2}$,
∴$BC^{2} + (\frac{1}{2}BC)^{2} = 6^{2}$,
解得$BC = \frac{12\sqrt{5}}{5}$
2. 解:
(1)如图1,点P即为所作;

(2)
∵点P是边AC关于边AB的“白银点”,
∴$AB^{2} = AP·AC$,
即$\frac{AP}{AB} = \frac{AB}{AC}$,又
∵∠A = ∠A,
∴△ABP∽△ACB,
∴$\frac{BP}{BC} = \frac{AB}{AC}$,
又
∵AB = 4,AC = 8,BC = 6,
∴$\frac{BP}{6} = \frac{4}{8}$,
∴BP = 3;
(3)①如图2,作∠BAC的平分线AD交BC于点D,

∴∠BAD = ∠CAD = $\frac{1}{2}$∠BAC,
又
∵∠BAC = 2∠C,
∴∠C = ∠CAD,
∴AD = CD,
∵∠ADB = ∠C + ∠CAD = 2∠C,
∴∠ADB = ∠BAC,
又
∵∠B = ∠B,
∴△BDA∽△BAC,
∴$\frac{BD}{BA} = \frac{BA}{BC} = \frac{AD}{AC}$,
∵AB = 4,BC = 6,
∴$BD = \frac{AB^{2}}{BC} = \frac{16}{6} = \frac{8}{3}$,
∴AD = CD = BC - BD = 6 - $\frac{8}{3} = \frac{10}{3}$,
∴$AC = \frac{AB×AD}{BD} = \frac{4×\frac{10}{3}}{\frac{8}{3}} = 5$;
②如图3,过点B作BD⊥AC于点D,

∴∠A + ∠ABD = 90°,
∵∠C = 45° - $\frac{1}{2}$∠A,
∴90° - ∠A = 2∠C,
∴∠ABD = 2∠C,
作∠ABD的平分线交AC于点E,
∴∠ABE = ∠DBE = $\frac{1}{2}$∠ABD,
∴∠ABE = ∠DBE = ∠C,
又
∵∠A = ∠A,
∴△ABE∽△ACB,
∴$\frac{AB}{AC} = \frac{AE}{AB} = \frac{BE}{BC}$,又
∵AB = 4,AC = 8,
∴AE = 2,CE = AC - AE = 8 - 2 = 6,$\frac{BE}{BC} = \frac{1}{2}$,
∴$BE = \frac{1}{2}BC$,又
∵∠C + ∠DBC = 90°,
∠DBE = ∠C,
∴∠DBE + ∠DBC = ∠DBC + ∠C = 90°,
∴BE⊥BC,
∴$BC^{2} + BE^{2} = CE^{2}$,
∴$BC^{2} + (\frac{1}{2}BC)^{2} = 6^{2}$,
解得$BC = \frac{12\sqrt{5}}{5}$
查看更多完整答案,请扫码查看


