《2026年全优中考系统总复习数学河北专版》

练 1 [25·陕西] 如图，正方形 $ ABCD $ 的边长为 4，点 $ E $ 为 $ AB $ 的中点，点 $ F $ 在 $ AD $ 上，$ EF \perp EC $，则 $ \triangle CEF $ 的面积为(C)

A.$ 10 $
B.$ 8 $
C.$ 5 $
D.$ 4 $

答案： 练1 C

练 2 [优质原创] 已知正方形 $ ABCD $，$ E $，$ F $ 为平面内两点。
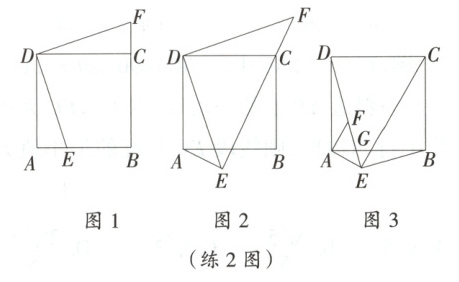
(1)如图 1，当点 $ E $ 在边 $ AB $ 上时，$ DE \perp DF $，且 $ B $，$ C $，$ F $ 三点共线。求证：$ AE = CF $；
(2)如图 2，当点 $ E $ 在正方形 $ ABCD $ 外部时，$ DE \perp DF $，$ AE \perp EF $，且 $ E $，$ C $，$ F $ 三点共线。猜想并证明线段 $ AE $，$ CE $，$ DE $ 之间的数量关系；
(3)如图 3，当点 $ E $ 在正方形 $ ABCD $ 外部时，$ AE \perp EC $，$ AE \perp AF $，$ DE \perp BE $，且 $ D $，$ F $，$ E $ 三点共线，$ DE $ 与 $ AB $ 交于点 $ G $。若 $ DF = 3 $，$ AE = \sqrt{2} $，求 $ EC $ 的长。

答案：
练2 解:
(1)证明:
∵四边形$ABCD$是正方形,
∴$DA=DC$,$\angle A=\angle ADC=\angle DCB=90°$,
∴$\angle DCF=90°$,
∵$DE\perp DF$,
∴$\angle EDF=\angle ADC=90°$,
∴$\angle ADE=\angle CDF$,
在$\triangle DAE$和$\triangle DCF$中,
$\begin{cases}\angle ADE=\angle CDF\\DA=DC\\\angle A=\angle DCF\end{cases}$
∴$\triangle DAE\cong\triangle DCF(ASA)$,
∴$AE=CF$;
(2)猜想:$AE+CE=\sqrt{2}DE$.
证明:
∵四边形$ABCD$是正方形,
∴$DA=DC$,$\angle ADC=90°$,
∵$DE\perp DF$,$AE\perp EF$,
∴$\angle AEF=\angle EDF=90°$,
∴$\angle ADC=\angle EDF$,
∴$\angle ADE=\angle CDF$,
∵$\angle ADC+\angle AEC=180°$,
∴$\angle DAE+\angle DCE=180°$,
∵$\angle DCF+\angle DCE=180°$,
∴$\angle DAE=\angle DCF$,
∴$\triangle DAE\cong\triangle DCF(ASA)$,
∴$AE=CF$,
$DE=DF$,
∴$EF=\sqrt{2}DE$,
∴$AE+CE=CE+CF=EF$,
∴$AE+CE=\sqrt{2}DE$;
(3)如图,连接$AC$,取$AC$的中点$O$,连接$OE$,$OD$.
∵四边形$ABCD$是正方形,$AE\perp EC$,
∴$\angle AEC=\angle ADC=90°$,
∵$OA=OC$,
∴$OD=OA=OC=OE$,
∴$A$,$E$,$C$,$D$四点共圆,
∴$\angle AED=\angle ACD=45°$,
∴$\angle AED=\angle DEC=45°$,由
(2)可知,
$AE+EC=\sqrt{2}DE$,
∵$AE\perp AF$,
∴$\angle EAF=90°$,$\angle AEF=\angle AFE=45°$,
∴$AE=AF=\sqrt{2}$,
∴$EF=\sqrt{2}AE=2$,
∵$DF=3$,$DE=5$,
∴$\sqrt{2}+EC=5\sqrt{2}$,
∴$EC=4\sqrt{2}$.