《2026年全优中考系统总复习数学河北专版》

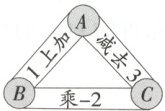
例1 有一个数学游戏，如图，一个实数从$A$，$B$，$C$三个位置中任选一个位置出发，按照通道内标注的要求进行运算后到下一个位置.例如：将$3$按照$B→C$（或$C→B$）的顺序进行运算，是将数据$3$经过“乘$-2$”的运算得出结果$-6$.
(1)将$-2$按照$A→B→C→A$的顺序进行运算，列出算式并求出运算结果；
(2)将一个大于$3$的数按照$A→C→B→A$的顺序进行运算，发现运算结果总小于$1$.请验证这个结论.

答案： 例1 解：
(1)根据题意列式为$(-2+1)× (-2)-3=-1×(-2)-3=-1$；
(2)设这个数为$x$，则$(x-3)×(-2)+1=-2x+7\because x＞3,\therefore -2x+7＜1$。

1. 计算：
(1)[25·北京]$\vert -3\vert +\sqrt{27}+(\dfrac{1}{2})^{-1}-2\sin 30^{\circ}$；
(2)[25·深圳]$\sqrt{16}+\vert -3\vert +(\pi - 3.14)^{0}+(-1)^{2025}$.

答案： 1. 解：
(1)原式$=3+3\sqrt{3}+2-2×\frac{1}{2}=3+3\sqrt{3}+2-1=4+3\sqrt{3}$；
(2)原式$=4+3+1-1=8-1=7$。

2. 小明使用比较简便的方法完成了一道作业题，如下图：

请你参考小明的方法计算：
(1)$4^{2025}× (-0.25)^{2025}$；
(2)$(\dfrac{12}{5})^{2023}× (-\dfrac{5}{6})^{2025}× (\dfrac{1}{2})^{2024}$.

答案： 2. 解：
(1)$4^{2025}×(-0.25)^{2025}=(-4×0.25)^{2025}=(-1)^{2025}=-1$；
(2)原式$=(-\frac{12}{5}×\frac{5}{6}×\frac{1}{2})^{2023}×(-\frac{5}{6})^2×\frac{1}{2}=-1×\frac{25}{36}×\frac{1}{2}=-\frac{25}{72}$。

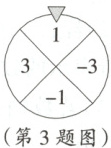
3. [25·石家庄44中三模]老师在黑板上写了一个不完整的算式：$-6 - □× 2 + 5$.转动转盘，转盘停止后将指针所指区域的数填入“$□$”内并完成算式计算，若指针指在边界线上无效.如图是第1次转动转盘，转盘停止后指针所指区域的情况.
(1)第1次转动转盘后，求算式的计算结果；
(2)某次转动转盘后，算式的计算结果是$-7$，求指针所指区域的数；
(3)多次转动（指针在每个区域至少停留一次）转盘并计算后发现，有一个计算结果最大.请直接写出这个最大的结果.

答案： 3. 解：
(1)$-6-1×2+5=-6-2+5=-3$；
(2)设指针所指区域的数为$x$，则$-6-x×2+5=-7$，$-2x=-6$，解得$x=3$，所以指针所指区域的数是$3$；
(3)5. 提示：$-6-1×2+5=-3$，$-6-(-1)×2+5=1$，$-6-3×2+5=-7$，$-6-(-3)×2+5=5$，所以最大的结果是$5$。