第167页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
例3 [25·石家庄长安区一模]已知整式$P = a^{2}+4a$,$Q = a - 1$.
(1)若$M = P - 8Q$,求整式$M$;
(2)对任意实数$a$,判断整式$M$的值能为负数吗?说明理由.
备考建议:涉及代数式的求值问题时,一定要先化简再代入求值,避免计算出错.
(1)若$M = P - 8Q$,求整式$M$;
(2)对任意实数$a$,判断整式$M$的值能为负数吗?说明理由.
备考建议:涉及代数式的求值问题时,一定要先化简再代入求值,避免计算出错.
答案:
例3 解:
(1)
∵$P=a^{2}+4a$,$Q=a - 1$,
∴$M=$ $P - 8Q=(a^{2}+4a)-8(a - 1)=a^{2}+4a - 8a + 8=$ $a^{2}-4a + 8$;
(2)对任意实数$a$,整式$M$的值不能为负数,理由:由
(1)知,$M=a^{2}-4a + 8=(a - 2)^{2}+4>0$,
∴对任意实数$a$,整式$M$的值不能为负数.
(1)
∵$P=a^{2}+4a$,$Q=a - 1$,
∴$M=$ $P - 8Q=(a^{2}+4a)-8(a - 1)=a^{2}+4a - 8a + 8=$ $a^{2}-4a + 8$;
(2)对任意实数$a$,整式$M$的值不能为负数,理由:由
(1)知,$M=a^{2}-4a + 8=(a - 2)^{2}+4>0$,
∴对任意实数$a$,整式$M$的值不能为负数.
1. [25·保定名校联考]定义新运算:对于任意$a$,$b$都有$a\#b = a(a - b)$,等式右边是通常的减法及乘法运算,例如:$2\#1 = 2×(2 - 1) = 2$.
(1)计算$(m + n)\#2n$;
(2)若$2\#5x$的值是$0$,求$x$的值.
(1)计算$(m + n)\#2n$;
(2)若$2\#5x$的值是$0$,求$x$的值.
答案:
1.解:
(1)原式$=(m + n)(m - n)=m^{2}-n^{2}$;
(2)根据新定义得出一元一次方程为$2(2 - 5x)=0$,解得$x=\frac{2}{5}$,即$x$的值为$\frac{2}{5}$.
(1)原式$=(m + n)(m - n)=m^{2}-n^{2}$;
(2)根据新定义得出一元一次方程为$2(2 - 5x)=0$,解得$x=\frac{2}{5}$,即$x$的值为$\frac{2}{5}$.
2. [25·石家庄模拟]老师给出一道数学题,由学生接力完成分式的计算,如图所示,每人只能看到前一人传过来的式子.

(1)这个“接力游戏”中计算错误的同学有
(2)请你写出正确的解答过程;
(3)从“$-1$,$0$,$1$”中选择一个合适的数作为$a$的值,代入求该分式的值.

(1)这个“接力游戏”中计算错误的同学有
乙、丁
;(2)请你写出正确的解答过程;
(3)从“$-1$,$0$,$1$”中选择一个合适的数作为$a$的值,代入求该分式的值.
答案:
2.解:
(1)乙、丁
(2)原式$=[\frac{a^{2}-2a}{a + 1}-\frac{(a - 1)(a + 1)}{a + 1}]÷\frac{a}{a + 1}=\frac{a^{2}-2a-(a^{2}-1)}{a + 1}÷\frac{a}{a + 1}=\frac{-2a + 1}{a + 1}×\frac{a + 1}{a}=\frac{-2a + 1}{a}$;
(3)由于$a + 1\neq0$,$a\neq0$,所以$a\neq - 1$,$a\neq0$,所以$a = 1$;当$a = 1$时,原式$=\frac{-2×1 + 1}{1}=-1$.
(1)乙、丁
(2)原式$=[\frac{a^{2}-2a}{a + 1}-\frac{(a - 1)(a + 1)}{a + 1}]÷\frac{a}{a + 1}=\frac{a^{2}-2a-(a^{2}-1)}{a + 1}÷\frac{a}{a + 1}=\frac{-2a + 1}{a + 1}×\frac{a + 1}{a}=\frac{-2a + 1}{a}$;
(3)由于$a + 1\neq0$,$a\neq0$,所以$a\neq - 1$,$a\neq0$,所以$a = 1$;当$a = 1$时,原式$=\frac{-2×1 + 1}{1}=-1$.
3. 如图1,2,约定:上方相邻两代数式之和等于这两代数式下方箭头共同指向的代数式.
(1)求代数式$M$;
(2)嘉嘉说,无论$x$取什么值,$M$的值一定大于$N$的值,嘉嘉的说法是否正确?请通过计算说明.
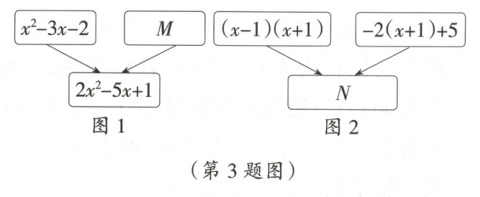
(1)求代数式$M$;
(2)嘉嘉说,无论$x$取什么值,$M$的值一定大于$N$的值,嘉嘉的说法是否正确?请通过计算说明.

答案:
3.解:
(1)由题意得$M = 2x^{2}-5x + 1-(x^{2}-3x - 2)=2x^{2}-5x + 1 - x^{2}+3x + 2=x^{2}-2x + 3$;
(2)正确,$N=(x - 1)(x + 1)-2(x + 1)+5=x^{2}-1 - 2x - 2 + 5=x^{2}-2x + 2$, $∴M - N=x^{2}-2x + 3-(x^{2}-2x + 2)=x^{2}-2x + 3 - x^{2}+2x - 2 = 1>0$,$∴M>N$.
(1)由题意得$M = 2x^{2}-5x + 1-(x^{2}-3x - 2)=2x^{2}-5x + 1 - x^{2}+3x + 2=x^{2}-2x + 3$;
(2)正确,$N=(x - 1)(x + 1)-2(x + 1)+5=x^{2}-1 - 2x - 2 + 5=x^{2}-2x + 2$, $∴M - N=x^{2}-2x + 3-(x^{2}-2x + 2)=x^{2}-2x + 3 - x^{2}+2x - 2 = 1>0$,$∴M>N$.
查看更多完整答案,请扫码查看


