《2025年绿色通道45分钟课时作业与单元测评高中数学必修第一册人教版》

1. 下列说法正确的是 (B)

A.终边相同的角一定相等
B.钝角一定是第二象限角
C.第一象限角一定不是负角
D.小于$90°$的角都是锐角

答案： 1.B 终边相同的角不一定相等，所以选项A错误；钝角一定是第二象限角，所以选项B正确；第一象限角可能是负角，如-330°是第一象限角，且是负角，所以选项C错误；小于90°的角不都是锐角，如-60°，所以选项D错误.

2. (2024·湖北荆州期末)与$-66°$角终边相同的角是 (D)

A.$34°$
B.$104°$
C.$214°$
D.$294°$

答案： 2.D 与-66°角终边相同的角可以写成$-66^{\circ}+360^{\circ}· k$，$k \in \mathbf{Z}$的形式.令k = 1，可得-66°角与294°角的终边相同，其他选项均不合题意.故选D.

3. (2024·山西大同一中月考)下列各角中是第二象限角的是 (C)

A.$420°$
B.$-75°$
C.$855°$
D.$-510°$

答案：
3.C $420^{\circ}=360^{\circ}+60^{\circ}$，$855^{\circ}=360^{\circ}×2 + 135^{\circ}$，$-510^{\circ}=-360^{\circ}-150^{\circ}$，如图所示，可知选C.

4. 终边与坐标轴重合的角$\alpha$的集合是 (C)

A.$\{\alpha|\alpha = k·360°,k\in\mathbf{Z}\}$
B.$\{\alpha|\alpha = k·180°,k\in\mathbf{Z}\}$
C.$\{\alpha|\alpha = k·90°,k\in\mathbf{Z}\}$
D.$\{\alpha|\alpha = k·180° + 90°,k\in\mathbf{Z}\}$

答案： 4.C 终边在坐标轴上的角为90°或90°的倍数角，所以终边与坐标轴重合的角α的集合为$\{ \alpha \mid \alpha = k · 90^{\circ} , k \in \mathbf{Z} \}$.

5. 已知集合$A = \{\alpha|45° + k·360°\leqslant\alpha\leqslant90° + k·360°,k\in\mathbf{Z}\}$，$B = \{\alpha|45° + k·180°\leqslant\alpha\leqslant90° + k·180°,k\in\mathbf{Z}\}$，则 (A)

A.$A\subseteq B$
B.$B\subseteq A$
C.$A = B$
D.$A\cap B=\varnothing$

答案： 5.A 当$k = 2n$，$n \in \mathbf{Z}$时，$B = \{ \alpha \mid 45^{\circ}+n·360^{\circ}\leqslant\alpha\leqslant90^{\circ}+n·360^{\circ} , n \in \mathbf{Z} \} = A$，当$k = 2n + 1$，$n \in \mathbf{Z}$时，$B = \{ \alpha \mid 225^{\circ}+n·360^{\circ}\leqslant\alpha\leqslant270^{\circ}+n·360^{\circ} , n \in \mathbf{Z} \}$，所以$A \subseteq B$.

6. 集合$\{\alpha|k·180°\leqslant\alpha\leqslant k·180° + 45°,k\in\mathbf{Z}\}$中角的

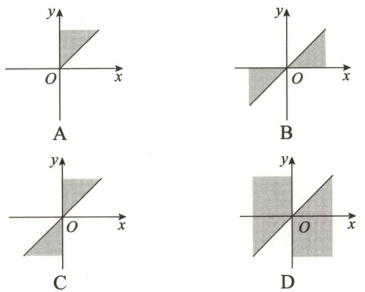
范

围是图中的(用阴影表示) (B)

答案： 6.B 集合$\{ \alpha \mid k · 180^{\circ}\leqslant\alpha\leqslant k · 180^{\circ}+45^{\circ} , k \in \mathbf{Z} \}$中，当k为偶数时，此集合与$\{ \alpha \mid 0^{\circ}\leqslant\alpha\leqslant45^{\circ} \}$表示终边相同的角，位于第一象限；当k为奇数时，此集合与$\{ \alpha \mid 180^{\circ}\leqslant\alpha\leqslant225^{\circ} \}$表示终边相同的角，位于第三象限.所以集合$\{ \alpha \mid k · 180^{\circ}\leqslant\alpha\leqslant k · 180^{\circ}+45^{\circ} , k \in \mathbf{Z} \}$中角的范围为选项B中阴影所示.

7. 如图，射线$OA$绕顶点$O$逆时针旋转$45°$到达$OB$位置，并在此基础上顺时针旋转$120°$到达$OC$位置，则$\angle AOC = $－75°.

答案： 7.－75°
解析 $\angle AOC = 45^{\circ}+(-120^{\circ})=-75^{\circ}$.

8. 与$-2025°$角的终边相同的最大负角是$-225^{\circ}$，与$2025°$角的终边相同的最小正角是$225^{\circ}$.

答案： 8.$-225^{\circ}$ $225^{\circ}$
解析 与－2025°角的终边相同的角的集合为$\{ \alpha \mid \alpha = k · 360^{\circ}-2025^{\circ} , k \in \mathbf{Z} \}$，则当k = 5时，$\alpha = 5×360^{\circ}-2025^{\circ}=-225^{\circ}$，此时为最大的负角.与2025°角的终边相同的角的集合为$\{ \beta \mid \beta = k · 360^{\circ}+2025^{\circ} , k \in \mathbf{Z} \}$，当k = －5时，$\beta = -5×360^{\circ}+2025^{\circ}=225^{\circ}$，此时为最小的正角.

9. 已知$\alpha = -1910°$。
(1) 把$\alpha$写成$\beta + k·360°(k\in\mathbf{Z},0\leqslant\beta\lt360°)$的形式，并指出它是第几象限角；
(2) 求$\theta$，使$\theta$与$\alpha$的终边相同，且$-720°\leqslant\theta\lt0°$。

答案： 9.解
(1)$\alpha = -1910^{\circ}=-6×360^{\circ}+250^{\circ}$，它是第三象限角.
(2)令$\theta = 250^{\circ}+n·360^{\circ}(n \in \mathbf{Z})$，
取n = －1，－2就得到符合$-720^{\circ}\leqslant\theta＜0^{\circ}$的角.
当n = －1时，$\theta = 250^{\circ}-360^{\circ}=-110^{\circ}$；
当n = －2时，$\theta = 250^{\circ}-720^{\circ}=-470^{\circ}$.
故$\theta = -110^{\circ}$或$\theta = -470^{\circ}$.

10. 在平面直角坐标系中，画出下列集合对应的区域（用阴影表示）：
(1) $\{\alpha|30° + k·360°\leqslant\alpha\leqslant60° + k·360°,k\in\mathbf{Z}\}$；
(2) $\{\alpha|30° + k·180°\leqslant\alpha\leqslant60° + k·180°,k\in\mathbf{Z}\}$。

答案：
10.解
(1)根据任意角的定义，画出集合$\{ \alpha \mid 30^{\circ}+k·360^{\circ}\leqslant\alpha\leqslant60^{\circ}+k·360^{\circ} , k \in \mathbf{Z} \}$对应的区域，如图1中阴影部分(含边界)所示。

(2)根据任意角的定义，画出集合$\{ \alpha \mid 30^{\circ}+k·180^{\circ}\leqslant\alpha\leqslant60^{\circ}+k·180^{\circ} , k \in \mathbf{Z} \}$对应的区域，如图2中阴影部分(含边界)所示。