2025年绿色通道45分钟课时作业与单元测评高中数学必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年绿色通道45分钟课时作业与单元测评高中数学必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
11. (2024·浙江杭州期中)若关于$x$的不等式$\frac{ax - 1}{x + b} > 0$的解集是$\{x\mid - 1 < x < 3\}$,则关于$x$的不等式$\frac{2ax + 1}{2x - b} < 0$的解集是 (
A.$\{x\mid -\frac{3}{2} < x < \frac{1}{2}\}$
B.$\{x\mid x < -\frac{3}{2} 或 x > \frac{1}{2}\}$
C.$\{x\mid -\frac{1}{2} < x < \frac{3}{2}\}$
D.$\{x\mid x < -\frac{1}{2} 或 x > \frac{3}{2}\}$
B
)A.$\{x\mid -\frac{3}{2} < x < \frac{1}{2}\}$
B.$\{x\mid x < -\frac{3}{2} 或 x > \frac{1}{2}\}$
C.$\{x\mid -\frac{1}{2} < x < \frac{3}{2}\}$
D.$\{x\mid x < -\frac{1}{2} 或 x > \frac{3}{2}\}$
答案:
11.B 因为$\frac {ax - 1}{x + b} > 0$等价于$(ax - 1)(x + b) > 0$,
所以$(ax - 1)(x + b) = 0$的两根为$\frac {1}{a}$,$- b$,
因为不等式解集为$\{ x\mid - 1 < x < 3\}$,
所以$a < 0$,所以$\frac {1}{a} = - 1$,$- b = 3$,
则$a = - 1$,$b = - 3$,
则$\frac {2ax + 1}{2x - b} < 0$即$\frac { - 2x + 1}{2x + 3} < 0$,等价于$(2x + 3)(2x - 1) > 0$,
解得$\begin{cases} x < - \frac {3}{2} \\或 x > \frac {1}{2} \end{cases}$.
所以$(ax - 1)(x + b) = 0$的两根为$\frac {1}{a}$,$- b$,
因为不等式解集为$\{ x\mid - 1 < x < 3\}$,
所以$a < 0$,所以$\frac {1}{a} = - 1$,$- b = 3$,
则$a = - 1$,$b = - 3$,
则$\frac {2ax + 1}{2x - b} < 0$即$\frac { - 2x + 1}{2x + 3} < 0$,等价于$(2x + 3)(2x - 1) > 0$,
解得$\begin{cases} x < - \frac {3}{2} \\或 x > \frac {1}{2} \end{cases}$.
12. 正数$a$,$b$满足$\frac{1}{a} + \frac{9}{b} = 1$,若不等式$a + b \geq - x^2 + 4x + 18 - m$对任意实数$x$恒成立,则实数$m$的取值范围是 (
A.$\{m\mid m \geq 3\}$
B.$\{m\mid m \leq 3\}$
C.$\{m\mid m \leq 6\}$
D.$\{m\mid m \geq 6\}$
D
)A.$\{m\mid m \geq 3\}$
B.$\{m\mid m \leq 3\}$
C.$\{m\mid m \leq 6\}$
D.$\{m\mid m \geq 6\}$
答案:
12.D $\because a > 0$,$b > 0$,$\frac {1}{a} + \frac {9}{b} = 1$,
$\therefore a + b = (a + b) \left( \frac {1}{a} + \frac {9}{b} \right) = 10 + \frac {b}{a} + \frac {9a}{b} \geq 10 + 2 \sqrt { \frac {b}{a} · \frac {9a}{b} } = 16$,
当且仅当$3a = b$,即$a = 4$,$b = 12$时,“$=$”成立.
若不等式$a + b \geq - x^2 + 4x + 18 - m$对任意实数$x$恒成立,
则$- x^2 + 4x + 18 - m \leq 16$,即$- x^2 + 4x + 2 \leq m$对任意实数$x$恒成立,只需$m \geq ( - x^2 + 4x + 2)_{\max}$.
$\because - x^2 + 4x + 2 = - (x - 2)^2 + 6 \leq 6$,$\therefore m \geq 6$,故选D.
$\therefore a + b = (a + b) \left( \frac {1}{a} + \frac {9}{b} \right) = 10 + \frac {b}{a} + \frac {9a}{b} \geq 10 + 2 \sqrt { \frac {b}{a} · \frac {9a}{b} } = 16$,
当且仅当$3a = b$,即$a = 4$,$b = 12$时,“$=$”成立.
若不等式$a + b \geq - x^2 + 4x + 18 - m$对任意实数$x$恒成立,
则$- x^2 + 4x + 18 - m \leq 16$,即$- x^2 + 4x + 2 \leq m$对任意实数$x$恒成立,只需$m \geq ( - x^2 + 4x + 2)_{\max}$.
$\because - x^2 + 4x + 2 = - (x - 2)^2 + 6 \leq 6$,$\therefore m \geq 6$,故选D.
13. 某服装公司生产的衬衫,在某城市年销售$8$万件,现该公司在该市设立代理商来销售衬衫,代理商向服装公司收取销售金额$r\%$的代理费。为此,该衬衫每件价格要提高到$\frac{80}{1 - r\%}$元才能保证公司利润。由于提价,每年将少销售$0.62r$万件,如果代理商每年收取的代理费不少于$16$万元,则$r$的取值范围是
$\frac {100}{31} \leq r \leq 10$
。
答案:
13.$\frac {100}{31} \leq r \leq 10$
解析 由题可知,提价后每年可销售$(8 - 0.62r)$万件,
所以$0 < r < \frac {400}{31}$,$1 - r\% · (8 - 0.62r) · r\% \geq 16$,
整理得,$3.1r^2 - 41r + 100 \leq 0$,解得$\frac {100}{31} \leq r \leq 10$.
解析 由题可知,提价后每年可销售$(8 - 0.62r)$万件,
所以$0 < r < \frac {400}{31}$,$1 - r\% · (8 - 0.62r) · r\% \geq 16$,
整理得,$3.1r^2 - 41r + 100 \leq 0$,解得$\frac {100}{31} \leq r \leq 10$.
14. 某企业计划加大对芯片研发部的投入,据了解,该企业芯片研发部原有$100$名技术人员,年人均投入$a(a > 0)$万元,现把原有技术人员分成两部分:技术人员和研发人员,其中技术人员$x$名($x \in N$且$45 \leq x \leq 75$),调整后研发人员的年人均投入增加$4x\%$,技术人员的年人均投入调整为$a\left(m - \frac{2x}{25}\right)$万元。
(1) 要使这$(100 - x)$名研发人员的年总投入不低于调整前$100$名技术人员的年总投入,求调整后的技术人员的人数最多是多少;
(2) 是否存在这样的实数$m$,使得技术人员在已知范围内调整后,同时满足以下两个条件:
① 技术人员的年人均投入始终不减少;② 研发人员的年总投入始终不低于技术人员的年总投入?
(1) 要使这$(100 - x)$名研发人员的年总投入不低于调整前$100$名技术人员的年总投入,求调整后的技术人员的人数最多是多少;
(2) 是否存在这样的实数$m$,使得技术人员在已知范围内调整后,同时满足以下两个条件:
① 技术人员的年人均投入始终不减少;② 研发人员的年总投入始终不低于技术人员的年总投入?
答案:
14.解
(1)依题意可得调整后研发人员的年人均投入为$(1 + 4x\%)a$万元,
则$(100 - x)(1 + 4x\%)a \geq 100a(a > 0)$,即$3x - \frac {x^2}{25} \geq 0$,解得$0 \leq x \leq 75$,
又$x \in N$且$45 \leq x \leq 75$,所以调整后的技术人员的人数最多为75.
(2)由①得$a \left( m - \frac {2x}{25} \right) \geq a$,解得$m \geq \frac {2x}{25} + 1$,
由②得$(100 - x)(1 + 4x\%)a \geq x \left( m - \frac {2x}{25} \right) a$,两边同时除以$ax$,得到$\left( \frac {100}{x} - 1 \right) \left( 1 + \frac {x}{25} \right) \geq m - \frac {2x}{25}$,整理得到$m \leq \frac {100}{x} + \frac {x}{25} + 3$,
故有$\frac {2x}{25} + 1 \leq m \leq \frac {100}{x} + \frac {x}{25} + 3$,
又$\frac {100}{x} + \frac {x}{25} + 3 \geq 2 \sqrt { \frac {100}{x} · \frac {x}{25} } + 3 = 7$,当且仅当$\frac {100}{x} = \frac {x}{25}$,
即$x = 50$时取等号,所以$m \leq 7$,
又因为$45 \leq x \leq 75$,所以当$x = 75$时,$\frac {2x}{25} + 1$取得最大值7,
所以$7 \leq m \leq 7$,
故存在$m = 7$满足条件.
(1)依题意可得调整后研发人员的年人均投入为$(1 + 4x\%)a$万元,
则$(100 - x)(1 + 4x\%)a \geq 100a(a > 0)$,即$3x - \frac {x^2}{25} \geq 0$,解得$0 \leq x \leq 75$,
又$x \in N$且$45 \leq x \leq 75$,所以调整后的技术人员的人数最多为75.
(2)由①得$a \left( m - \frac {2x}{25} \right) \geq a$,解得$m \geq \frac {2x}{25} + 1$,
由②得$(100 - x)(1 + 4x\%)a \geq x \left( m - \frac {2x}{25} \right) a$,两边同时除以$ax$,得到$\left( \frac {100}{x} - 1 \right) \left( 1 + \frac {x}{25} \right) \geq m - \frac {2x}{25}$,整理得到$m \leq \frac {100}{x} + \frac {x}{25} + 3$,
故有$\frac {2x}{25} + 1 \leq m \leq \frac {100}{x} + \frac {x}{25} + 3$,
又$\frac {100}{x} + \frac {x}{25} + 3 \geq 2 \sqrt { \frac {100}{x} · \frac {x}{25} } + 3 = 7$,当且仅当$\frac {100}{x} = \frac {x}{25}$,
即$x = 50$时取等号,所以$m \leq 7$,
又因为$45 \leq x \leq 75$,所以当$x = 75$时,$\frac {2x}{25} + 1$取得最大值7,
所以$7 \leq m \leq 7$,
故存在$m = 7$满足条件.
15. 数学中有些优美的曲线显示了数学形象美、对称美、和谐美,曲线$C$:$(x^2 + y^2)^3 = 16x^2y^2$就是四叶玫瑰线,则不等式$(x^2 + y^2)^3 \leq 16x^2y^2$表示区域所含的整点(即横、纵坐标均为整数的点)的个数为 (
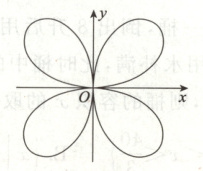
A.$1$
B.$4$
C.$5$
D.$9$
C
)
A.$1$
B.$4$
C.$5$
D.$9$
答案:
15.C 因为$\sqrt {x^2y^2} \leq \frac {x^2 + y^2}{2}$,所以$(x^2 + y^2)^3 \leq 16x^2y^2$可化为$(x^2 + y^2)^3 \leq 16 \left( \frac {x^2 + y^2}{2} \right)^2$,得$x^2 + y^2 \leq 4$,当且仅当$x^2 = y^2$时取等号,经检验,只有$(1,1)$,$(1, - 1)$,$( - 1,1)$,$( - 1, - 1)$和$(0,0)$共5个整点满足$(x^2 + y^2)^3 \leq 16x^2y^2$.故选C.
查看更多完整答案,请扫码查看


