《2025年绿色通道45分钟课时作业与单元测评高中数学必修第一册人教版》

10. 为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用 20 年的隔热层，隔热层建造成本为 6 万元/cm。该建筑物每年的能源消耗费用$ C $（单位：万元）与隔热层厚度$ x $（单位：cm）满足关系：$ C(x) = \dfrac{40}{3x + 5} $（$ 1 \leqslant x \leqslant 10 $），设$ y $为隔热层建造费用与 20 年的能源消耗费用之和。
（1）求$ y $关于$ x $的关系式；
（2）隔热层修

建

多厚时，总费用$ y $达到最小？并求最小值。

答案： 10.解
(1)由题意可知$y=20× \frac{40}{3x+5} +6x=\frac{800}{3x+5} +6x(1\leq x\leq 10)$.
(2)由
(1)知$y=\left( \frac{800}{3x+5} +6x+10\right)-10\geq 2\sqrt{1600}-10=70$，
当且仅当$\frac{800}{3x+5}=6x+10$，即$x=5$时取等号，
所以当隔热层厚度为$5 cm$时总费用$y$最小，最小值为$70$万元.

11. 制作一个面积为$ 2\ m^2 $，形状为直角三角形的铁支架框，有下列四种长度的铁管供选择，较经济(够用，又耗材最少)的是 (C)

A.6.2 m
B.6.8 m
C.7 m
D.7.2 m

答案： 11.C 设两直角边的长度分别为$a$，$b$，$a＞0$，$b＞0$，则$ab = 4$，铁支架框的周长$l=a+b+\sqrt{a^2+b^2}\geq 2\sqrt{ab}+\sqrt{2ab}=4+2\sqrt{2}\approx 6.828$，当且仅当$a=b=2$时取等号.故选C.

12. (2024·山东济南期末)假设某条道路一小时通过的车辆数$ N $满足关系$ N = \dfrac{5\ 000v}{\dfrac{7}{2}v + \dfrac{3}{2}v^2 + 5d_0} $，其中$ d_0 $为安全距离(单位：m)，$ v $为车速(单位：m/s)。当安全距离$ d_0 $取 30 m 时，$ N $的最大值约为 (B)

A.125
B.149
C.160
D.190

答案： 12.B 由题意得$N=\frac{\frac{5000}{v}}{ \frac{7}{2}v+\frac{3}{2}v^2+150} =\frac{\frac{5000}{v}}{\frac{7}{2}v+\frac{3}{2}v^2+30}\leq \frac{\frac{5000}{v}}{2\sqrt{\frac{7}{2}v· \frac{3}{2}v^2}+30} \approx 149$当且仅当$\frac{\frac{7}{2}v+2\sqrt{\frac{3}{2}v· \frac{150}{v}}}{\frac{5000}{v}} =\frac{\frac{7}{2}v+30}{\frac{5000}{v}}$，即$v = 10$时取等号)，故选B.

13. 若某商品进货价为每件 10 元，当销售价格(每件$ x $元)在$ 10 ＜ x \leqslant 25 $时，售出的件数$ P = \dfrac{10^4}{(x - 5)^2} $。若想利润最大，则销售价格应定为每件15 元。

答案： 13.15
解析 由题意可知，利润为$\frac{10^4(x - 10)}{(x - 5)^2}$，$10＜x\leq 25$，
不妨令$t=x - 10\in \{t\mid 0＜t\leq 15\}$，
则利润为$\frac{10^4t}{(t + 5)^2} =\frac{10^4t}{t^2+10t+25} \leq \frac{10^4}{2\sqrt{t· \frac{25}{t}}+10} =500$，
当且仅当$t=\frac{25}{t}$，即$t=5$时取等号，此时$x=15$，
故销售价格应定为每件$15$元.

14. （链接教材 P49 习题 2.2 T8）某公园内有一块场地，如图所示，当地的文旅集团欲把$ \triangle ACD $，$ \triangle ABD $，$ \triangle BDE $三块区域种植不同的花草供游客欣赏，已知$ \angle ACB = \angle AEB = 90° $，$ AC = BE $，$ CA + CB = 4\ km $，设$ BC = x\ km $。
（1）请用$ x $表示$ CD $；
（2）当$ x $取何值时，$ \triangle ACD $的面积最大？并求最大面积。

答案： 14.解
(1)因为$\angle ACB=\angle AEB=90°$，$AC=BE=4 - x$，$\angle CDA=\angle EDB$，所以直角三角形$ACD$与直角三角形$BED$全等，所以$CD=DE$.在$Rt\triangle BDE$中，$BD^2=ED^2+$
$EB^2$，所以$(x - CD)^2=CD^2+(4 - x)^2$，整理得$CD=4 - \frac{8}{x}(0＜x＜4)$.
(2)由
(1)得$\triangle ACD$的面积为$S_{\triangle ACD}=\frac{1}{2}AC· CD=\frac{1}{2}(4 - x)\left( 4 - \frac{8}{x}\right)=12 - \left( 2x+\frac{16}{x}\right)\leq 12 - 2\sqrt{2x· \frac{16}{x}}=12 - 8\sqrt{2}$，当且仅当$2x=\frac{16}{x}$，即$x=2\sqrt{2}$时等号成立，所以当$x=2\sqrt{2}$时，$\triangle ACD$的面积最大，最大面积为$(12 - 8\sqrt{2}) km^2$.

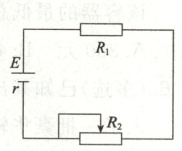
15. (知识交汇)如图，电路中电源的电动势为$ E $，内阻为$ r $，$ R_1 $为固定电阻，$ R_2 $是一个滑动变阻器，已知$ R_2 $消耗的电功率为$ P = \left( \dfrac{E}{r + R_1 + R_2} \right)^2 R_2 $，当$ R_2 $消耗的电功率$ P $最大时，$ r $，$ R_1 $，$ R_2 $之间的关系是 (B)

A.$ r + R_2 = R_1 $
B.$ r + R_1 = R_2 $
C.$ \dfrac{R_1}{r} = R_2 $
D.$ R_1 + R_2 = r $

答案： 15.B 由题意，$P=\left( \frac{E}{r+R_1+R_2}\right)R_2$
$=\frac{E^2R_2}{(r+R_1)^2+2(r+R_1)+R_2^2}$
$=\frac{E^2R_2}{(r+R_1)^2+R_2+2(r+R_1)}$
$\because \frac{(r+R_1)^2}{R_2}+R_2\geq 2\sqrt{\frac{(r+R_1)^2}{R_2}· R_2}=2(r+R_1)$，当且仅当$\frac{(r+R_1)^2}{R_2}=R_2$，即$r+R_1=R_2$时取等号，
$\therefore$当$r+R_1=R_2$时，$P$取得最大值$\frac{E^2}{4(r+R_1)}$.故选B.