《2025年绿色通道45分钟课时作业与单元测评高中数学必修第一册人教版》

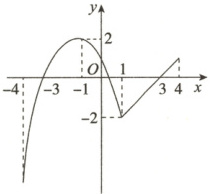
1. 若函数$ f(x) $的图象如图所示，则其单调递减区间是(B)


A.$[-4,-1],[1,4]$
B.$[-1,1]$
C.$[-4,4]$
D.$[-2,2]$

答案： 1.B　观察函数f(x)的图象，可知函数f(x)的单调递减区间为[−1,1].

2. (多选)下列函数在区间$(0,1)$上单调递增的是(BD)

A.$ y = 1 - 2x $
B.$ y = -\dfrac{1}{x + 1} $
C.$ y = x^2 - 2x $
D.$ y = -x^2 + 2x $

答案： 2.BD　显然y=1−2x在(0,1)上单调递减;
∵t=$\frac{1}{x+1}$在(0,1)上单调递减，
∴y=−$\frac{1}{x+1}$在(0,1)上单调递增;
　y=x²−2x=(x−1)²−1的图象关于x=1对称,且图象为开口向上的抛物线，
∴y=x²−2x在(0,1)上单调递减;
　由y=−x²+2x=−(x−1)²+1知,图象关于x=1对称，且图象为开口向下的抛物线，
∴y=−x²+2x在(0,1)上单调递增.故选BD.

3. 若函数$ y = x^2 + (2a - 1)x + 1 $在区间$(-\infty, 2]$上是减函数，则实数$ a $的取值范围是(B)

A.$\left(-\dfrac{3}{2}, +\infty\right)$
B.$\left(-\infty, -\dfrac{3}{2}\right]$
C.$(3, +\infty)$
D.$(-\infty, -3]$

答案： 3.B
∵函数y=x²+(2a−1)x+1的图象是开口向上的抛物线，直线x=$\frac{1 - 2a}{-2}$为图象的对称轴，函数在区间(−∞,2]上是减函数，
∴2≤$\frac{1 - 2a}{-2}$，解得a≤−$\frac{3}{2}$.

4. 若函数$ f(x) $在$(-\infty, -1]$上是增函数，则下列关系式中成立的是(D)

A.$ f\left(-\dfrac{3}{2}\right) ＜ f(-1) ＜ f(-2) $
B.$ f(-1) ＜ f\left(-\dfrac{3}{2}\right) ＜ f(-2) $
C.$ f(-2) ＜ f(-1) ＜ f\left(-\dfrac{3}{2}\right) $
D.$ f(-2) ＜ f\left(-\dfrac{3}{2}\right) ＜ f(-1) $

答案： 4.D
∵f(x)在(−∞,−1]上是增函数,且−2＜−$\frac{3}{2}$＜−1,
∴f(−2)＜f(−$\frac{3}{2}$)＜f(−1).

5. (2025·江西南昌期中)设$ f(x) $是$ \mathbf{R} $上的减函数，则不等式$ f(2) ＜ f\left(\dfrac{1}{x}\right) $的解集是(D)

A.$ \left(0, \dfrac{1}{2}\right) $
B.$ \left(-\infty, \dfrac{1}{2}\right) $
C.$ \left(\dfrac{1}{2}, +\infty\right) $
D.$ (-\infty, 0) \cup \left(\dfrac{1}{2}, +\infty\right) $

答案： 5.D
∵f(x)是R上的减函数,且f
(2)＜f($\frac{1}{x}$),
∴2＞$\frac{1}{x}$,
∴x＜0或x＞$\frac{1}{2}$,故选D.

6. (多选)已知函数$ f(x) $在$ \mathbf{R} $上是减函数，且$ a + b ＞ 0 $，则下列说法正确的是(CD)

A.$ f(a) + f(b) ＞ 0 $
B.$ f(a) - f(-b) ＞ 0 $
C.$ f(-a) - f(b) ＞ 0 $
D.$ f(a) + f(b) ＜ f(-a) + f(-b) $

答案： 6.CD　由a+b＞0,得a＞−b,b＞−a,
　因为函数f(x)在R上是减函数,所以f(a)＜f(−b),f(b)＜f(−a),则f(−a)−f(b)＞0,f(a)+f(b)＜f(−a)+f(−b).故选CD.

7. 若函数$ f(x) $满足：对任意的$ x_1, x_2 \in \mathbf{R} $都有$ (x_1 - x_2)[f(x_1) - f(x_2)] ＞ 0 $，则$ f(-3) $与$ f(-\pi) $的大小关系是f(−3)＞f(−π)。

答案： 7.f(−3)＞f(−π)
　解析
∵∀x₁,x₂∈R都有(x₁−x₂)[f(x₁)−f(x₂)]＞0,
∴f(x)在R上是增函数，
∵−3＞−π,
∴f(−3)＞f(−π).

8. 函数$ f(x) = \begin{cases}x^2 + 1, & x \geq 0, \\ 1 - x^2, & x ＜ 0\end{cases}$在$ \mathbf{R} $上 ______ (填“单调递增”“单调递减”“先增后减”或“先减后增”)。

答案： 8.单调递增
　解析　当x∈[0,+∞)时,f(x)=x²+1单调递增，且f(x)≥1.又在区间(−∞,0)上,f(x)=1−x²单调递增,且f(x)＜1,故f(x)在R上单调递增.

9. 已知函数$ f(x) = \begin{cases} x, & x \in [0, 2], \\ \dfrac{4}{x}, & x \in (2, 4]. \end{cases} $
（1）画出函数$ f(x) $的大致图象；
（2）写出函数$ f(x) $的单调递减区间。

答案：
9.解　
(1)函数f(x)的大致图象如图所示.
　　　　　　　　
(2)由函数f(x)的图象得出，函数的单调递减区间为[2,4].