2024年绿色通道45分钟课时作业与单元测评数学选择性必修第二册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2024年绿色通道45分钟课时作业与单元测评数学选择性必修第二册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列有关数列的说法正确的是 ( )
A. 同一数列的任意两项均不可能相同
B. 数列-1,0,1与数列1,0,-1是同一个数列
C. 数列1,3,5,7可表示为{1,3,5,7}
D. 数列2,5,2,5,…,2,5,…是无穷数列
A. 同一数列的任意两项均不可能相同
B. 数列-1,0,1与数列1,0,-1是同一个数列
C. 数列1,3,5,7可表示为{1,3,5,7}
D. 数列2,5,2,5,…,2,5,…是无穷数列
答案:
D 无穷个3构成的常数数列3,3,3, …的各项都是3,故A错误;数列−1,0,1与数列1,0, −1项的顺序不同,即表示不同的数列,故B错误;{1,3,5,7}是一个集合,故C错误;根据数列的分类,数列2,5,2,5, …,2,5, …中的项有无穷多个,所以是无穷数列,故D正确. 故选D.
2.(2023·四川树德中学期中)已知数列{an}的通项公式为an=sin$\frac{n\pi }{3}$,则a2 023的值为 ( )
A. $\frac{\sqrt{3}}{2}$
B. 0
C. -$\frac{\sqrt{3}}{2}$
D. $\frac{1}{2}$
A. $\frac{\sqrt{3}}{2}$
B. 0
C. -$\frac{\sqrt{3}}{2}$
D. $\frac{1}{2}$
答案:
A 由题意得$a_{1}=\frac{\sqrt{3}}{2},a_{2}=\frac{\sqrt{3}}{2},a_{3}=0,a_{4}=-\frac{\sqrt{3}}{2},a_{5}=-\frac{\sqrt{3}}{2},a_{6}=0,a_{7}=\frac{\sqrt{3}}{2},\cdots$,所以数列$\{a_{n}\}$的周期为6,又$2023 = 6×337 + 1$,所以$a_{2023}=a_{1}=\frac{\sqrt{3}}{2}$.
3.(2024·河南南阳一中月考)已知数列$\sqrt{2}$,2,2$\sqrt{2}$,4,…,则16$\sqrt{2}$是这个数列的 ( )
A. 第8项
B. 第9项
C. 第10项
D. 第11项
A. 第8项
B. 第9项
C. 第10项
D. 第11项
答案:
B 将数列改写为$\sqrt{2},(\sqrt{2})^{2},(\sqrt{2})^{3},(\sqrt{2})^{4},\cdots$,由此可归纳该数列的通项公式为$a_{n}=(\sqrt{2})^{n}(n\in\mathbf{N}^{*})$. 又$16\sqrt{2}=(\sqrt{2})^{9}$,所以$16\sqrt{2}$是这个数列的第9项. 故选B.
4.(多选)已知数列{an}的前4项分别为1,0,1,0,则下列通项公式可以作为数列{an}的通项公式的是 ( )
A. an=$\frac{1}{2}$[1+(-1)n+1]
B. an=sin2$\frac{n\pi }{2}$
C. an=$\left\{\begin{array}{l}1,n为奇数,\\ 0,n为偶数\end{array}\right.$
D. an=$\frac{1}{2}$[1+(-1)n+1]+(n-1)(n-2)
A. an=$\frac{1}{2}$[1+(-1)n+1]
B. an=sin2$\frac{n\pi }{2}$
C. an=$\left\{\begin{array}{l}1,n为奇数,\\ 0,n为偶数\end{array}\right.$
D. an=$\frac{1}{2}$[1+(-1)n+1]+(n-1)(n-2)
答案:
ABC 对于A,$a_{1}=\frac{1}{2}\times(1 + 1)=1,a_{2}=\frac{1}{2}\times(1 - 1)=0,a_{3}=\frac{1}{2}\times(1 + 1)=1,a_{4}=\frac{1}{2}\times(1 - 1)=0$,符合;
对于B,$a_{1}=\sin^{2}\frac{\pi}{2}=1,a_{2}=\sin^{2}\pi=0,a_{3}=\sin^{2}\frac{3\pi}{2}=1,a_{4}=\sin^{2}2\pi=0$,符合;
对于C,$a_{1}=1,a_{2}=0,a_{3}=1,a_{4}=0$,符合;
对于D,$a_{1}=\frac{1}{2}\times(1 + 1)+0\times(-1)=1,a_{2}=\frac{1}{2}\times(1 - 1)+1\times0=0,a_{3}=\frac{1}{2}\times(1 + 1)+2\times1=3,a_{4}=\frac{1}{2}\times(1 - 1)+3\times2=6$,不符合. 故选ABC.
对于B,$a_{1}=\sin^{2}\frac{\pi}{2}=1,a_{2}=\sin^{2}\pi=0,a_{3}=\sin^{2}\frac{3\pi}{2}=1,a_{4}=\sin^{2}2\pi=0$,符合;
对于C,$a_{1}=1,a_{2}=0,a_{3}=1,a_{4}=0$,符合;
对于D,$a_{1}=\frac{1}{2}\times(1 + 1)+0\times(-1)=1,a_{2}=\frac{1}{2}\times(1 - 1)+1\times0=0,a_{3}=\frac{1}{2}\times(1 + 1)+2\times1=3,a_{4}=\frac{1}{2}\times(1 - 1)+3\times2=6$,不符合. 故选ABC.
5. 下列各数中,是数列{n2+4}中的项的是 ( )
A. 90
B. 29
C. 30
D. 23
A. 90
B. 29
C. 30
D. 23
答案:
B 令$n^{2}+4 = 29$,即$n^{2}=25$,解得$n = 5$或$n=-5$(舍去),则29是数列$\{n^{2}+4\}$中的第5项. 故选B.
6. 观察数列21,ln 2,cos 3,24,ln 5,cos 6,27,ln 8,cos 9,…,则该数列的第20项为 ( )
A. 220
B. 20
C. ln 20
D. cos 20
A. 220
B. 20
C. ln 20
D. cos 20
答案:
C 观察数列,可知数列中的项中的指数、真数、弧度数是按1,2,3, …排列的,且以3为周期依次取指数值、对数值、余弦值,因为$20 = 6×3+2$,所以第20项为$\ln20$. 故选C.
7. 数列{an}的通项公式为an=log(n+1)(n+2),则它前14项的积为________.
答案:
4
解析 $\log_{2}3\times\log_{3}4\times\log_{4}5\times\cdots\times\log_{15}16=\log_{2}16 = 4$.
解析 $\log_{2}3\times\log_{3}4\times\log_{4}5\times\cdots\times\log_{15}16=\log_{2}16 = 4$.
8. 已知数列{an}的通项公式为an=$\frac{1}{\sqrt{n}+\sqrt{n + 1}}$,则$\sqrt{10}$-3是此数列的第________项.
答案:
9
解析 $a_{n}=\frac{1}{\sqrt{n}+\sqrt{n + 1}}=\sqrt{n + 1}-\sqrt{n}$,$\because\sqrt{10}-3=\sqrt{9 + 1}-\sqrt{9}$,$\therefore\sqrt{10}-3$是数列$\{a_{n}\}$的第9项.
解析 $a_{n}=\frac{1}{\sqrt{n}+\sqrt{n + 1}}=\sqrt{n + 1}-\sqrt{n}$,$\because\sqrt{10}-3=\sqrt{9 + 1}-\sqrt{9}$,$\therefore\sqrt{10}-3$是数列$\{a_{n}\}$的第9项.
9. 根据下列数列{an}的通项公式,写出数列的前5项,并作出它们的图象.
(1)an=$\frac{1}{2}$n-1;(2)an=sin$\frac{(n + 2)\pi }{2}$.
(1)an=$\frac{1}{2}$n-1;(2)an=sin$\frac{(n + 2)\pi }{2}$.
答案:
解 (1)当通项公式中的$n = 1,2,3,4,5$时,数列$\{a_{n}\}$的前5项依次为$-\frac{1}{2},0,\frac{1}{2},1,\frac{3}{2}$. 图象如图1所示.
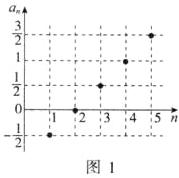
(2)当通项公式中的$n = 1,2,3,4,5$时,数列$\{a_{n}\}$的前5项依次为−1,0,1,0, −1. 图象如图2所示.

解 (1)当通项公式中的$n = 1,2,3,4,5$时,数列$\{a_{n}\}$的前5项依次为$-\frac{1}{2},0,\frac{1}{2},1,\frac{3}{2}$. 图象如图1所示.

(2)当通项公式中的$n = 1,2,3,4,5$时,数列$\{a_{n}\}$的前5项依次为−1,0,1,0, −1. 图象如图2所示.

10. 已知数列{an}的通项公式为an=$\frac{n^{2}-21n}{2}$.
(1)判断0和1是不是数列{an}的项,若是,指出是第几项;若不是,请说明理由.
(2)判断数列{an}中是否存在连续且相等的两项,若存在,指出分别是哪两项;若不存在,请说明理由.
(1)判断0和1是不是数列{an}的项,若是,指出是第几项;若不是,请说明理由.
(2)判断数列{an}中是否存在连续且相等的两项,若存在,指出分别是哪两项;若不存在,请说明理由.
答案:
解 (1)令$a_{n}=0$,得$n^{2}-21n = 0$,
所以$n = 21$或$n = 0$(舍去),所以0是数列$\{a_{n}\}$的项,且是第21项.
令$a_{n}=1$,得$\frac{n^{2}-21n}{2}=1$,该方程无正整数解,
所以1不是数列$\{a_{n}\}$的项.
(2)解法一:假设存在连续且相等的两项$a_{m},a_{m + 1},m\in\mathbf{N}^{*}$,则有$a_{m}=a_{m + 1}$,
即$\frac{m^{2}-21m}{2}=\frac{(m + 1)^{2}-21(m + 1)}{2}$,解得$m = 10$,
所以数列$\{a_{n}\}$中存在连续且相等的两项,它们分别是第10项和第11项.
解法二:令$f(x)=\frac{x^{2}-21x}{2}$,则其图象的对称轴为直线$x = 10.5$,所以$f(10)=f(11)$,即$a_{10}=a_{11}$,所以数列$\{a_{n}\}$中存在连续且相等的两项,它们分别是第10项和第11项.
所以$n = 21$或$n = 0$(舍去),所以0是数列$\{a_{n}\}$的项,且是第21项.
令$a_{n}=1$,得$\frac{n^{2}-21n}{2}=1$,该方程无正整数解,
所以1不是数列$\{a_{n}\}$的项.
(2)解法一:假设存在连续且相等的两项$a_{m},a_{m + 1},m\in\mathbf{N}^{*}$,则有$a_{m}=a_{m + 1}$,
即$\frac{m^{2}-21m}{2}=\frac{(m + 1)^{2}-21(m + 1)}{2}$,解得$m = 10$,
所以数列$\{a_{n}\}$中存在连续且相等的两项,它们分别是第10项和第11项.
解法二:令$f(x)=\frac{x^{2}-21x}{2}$,则其图象的对称轴为直线$x = 10.5$,所以$f(10)=f(11)$,即$a_{10}=a_{11}$,所以数列$\{a_{n}\}$中存在连续且相等的两项,它们分别是第10项和第11项.
查看更多完整答案,请扫码查看


