《2025年绿色通道45分钟课时作业与单元测评高中数学必修第一册人教版》

1. (多选)下列关于不等关系的说法正确的是 (ACD)

A.某隧道入口竖立着“限高4.5米”的警示牌，是指示司机要安全通过隧道，应使车载货物高度$ h $(米)满足$ h \leq 4.5 $
B.用不等式表示“$ a $与$ b $的差不小于$ c $”为$ a - b ＞ c $
C.不等式$ x \geq 2 $的含义是指$ x $不小于2
D.若$ a ＜ b $或$ a = b $之中有一个正确，则$ a \leq b $正确

答案： 1.ACD 因为“限高4.5米”即为“高度不超过4.5米”，不超过用“$\leq$”表示，故选项A正确；因为“不小于”用“$\geq$”表示，所以$a - b \geq c$，故选项B错误；因为不等式$x \geq 2$表示$x ＞ 2$或$x = 2$，即$x$不小于2，故选项C正确；因为不等式$a \leq b$表示$a ＜ b$或$a = b$，故若$a ＜ b$或$a = b$中有一个正确，则$a \leq b$一定正确，故选项D正确.故选ACD.

2. 在开山工程爆破时，已知导火索燃烧的速度是每秒$ \frac{1}{2} $厘米，人跑开的速度是每秒4米，为了使点燃导火索的人能够在爆破时跑到100米以外的安全区，导火索的长度$ x $(厘米)应该满足的不等式为 (C)

A.$ 4 × 2x \geq 100 $
B.$ 4 × 2x \leq 100 $
C.$ 4 × 2x ＞ 100 $
D.$ 4 × 2x ＜ 100 $

答案： 2.C 当导火索的长度为$x$厘米时，燃烧的时间为$2x$秒，人跑开的距离为$4 × 2x$米，为了保证安全，有$4 × 2x ＞ 100$.

3. 19世纪戴德金利用他提出的分割理论，从对有理数集的分割精确地给出了实数的定义，并且该定义作为现代数学实数理论的基础之一可以推出实数理论中的六大基本定理，那么在证明有理数的不完备性时，经常会用到以下两个式子，已知正有理数$ p $，满足$ p^2 ＜ 2 $，$ q = p - \frac{p^2 - 2}{p + 2} $，则$ p $与$ q $的大小关系为 (A)

A.$ p ＜ q $
B.$ p ＞ q $
C.$ p = q $
D.无法判断

答案： 3.A 因为$p - q = p - p + \frac{p^{2} - 2}{p + 2} = \frac{p^{2} - 2}{p + 2}$，而$p^{2} ＜ 2,p ＞ 0$，所以$\frac{p^{2} - 2}{p + 2} ＜ 0$，即$p ＜ q$，故A正确.

4. 设$ M = 2a(a - 2) + 7 $，$ N = (a - 2)(a - 3) $，则$ M $与$ N $的大小关系是 (A)

A.$ M ＞ N $
B.$ M \geq N $
C.$ M ＜ N $
D.$ M \leq N $

答案： 4.A 因为$M - N = 2(a - 2) + 7 - (a - 2)(a - 3) = a^{2} + a + 1 = (a + \frac{1}{2})^{2} + \frac{3}{4} ＞ 0$，所以$M ＞ N$.

5. (2024·山东菏泽期中)若$ a ＞ b ＞ 0 $，且$ a + b = 1 $，则在下列四个选项中，最大的是 (C)

A.$ \frac{1}{2} $
B.$ a^2 + b^2 $
C.$ a $
D.$ 2ab $

答案： 5.C $\because a ＞ b ＞ 0$且$a + b = 1$，$\therefore a ＞ \frac{1}{2} ＞ b ＞ 0$，可排除A；又$2b ＜ 1 \Rightarrow 2ab ＜ a$，排除D；$\because a^{2} + b^{2} - a = (a + b)^{2} - 2ab - a = 1 - 2ab - a = a + b - 2ab - a = b - 2ab = b(1 - 2a) ＜ 0$，$\therefore a^{2} + b^{2} ＜ a$，排除B.故选C.

6. 已知$ 0 ＜ a ＜ \frac{1}{2} $，若$ A = 1 + a^2 $，$ B = \frac{1}{1 - a} $，则$ A $与$ B $的大小关系是 (A)

A.$ A ＜ B $
B.$ A ＞ B $
C.$ A = B $
D.不确定

答案： 6.A $A - B = 1 + a^{2} - \frac{1}{1 - a} - \frac{(1 + a^{2})(1 - a) - 1}{1 - a} = \frac{a^{2} - a - a^{3}}{1 - a} - \frac{a(a - 1 - a^{2})}{1 - a}$，因为$0 ＜ a ＜ \frac{1}{2}$，所以$1 - a ＞ 0$，又因为$a - 1 - a^{2} = - (a - \frac{1}{2})^{2} - \frac{3}{4} \leq - \frac{3}{4} ＜ 0$，所以$A - B ＜ 0$，即$A ＜ B$.

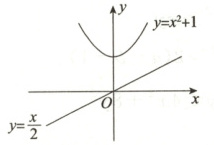
7. (2025·辽宁沈阳期末)用不等式表示图中两个函数之间的关系为$x^{2} + 1 ＞ \frac{x}{2}$.

答案： 7.$x^{2} + 1 ＞ \frac{x}{2}$
解析 $y = x^{2} + 1$的图象始终在$y = \frac{x}{2}$的图象的上方，也就是说$y = x^{2} + 1$的函数值总是大于$y = \frac{x}{2}$的函数值，即$x^{2} + 1 ＞ \frac{x}{2}$.

8. 若实数$ a ＞ b $，则$ a^2 - ab $＞ $ ba - b^2 $(填“＞”或“＜”).

答案： 8.＞
解析 因为$(a^{2} - ab) - (ba - b^{2}) = (a - b)^{2}$，又$a ＞ b$，所以$(a - b)^{2} ＞ 0$，所以$a^{2} - ab ＞ ba - b^{2}$.

9. 设$ a ＞ b ＞ 0 $，比较$ \frac{a^2 - b^2}{a^2 + b^2} $与$ \frac{a - b}{a + b} $的大小.

答案： 9.解 $\because a ＞ b ＞ 0 \Rightarrow a + b ＞ 0,a - b ＞ 0$，$\therefore \frac{a^{2} - b^{2}}{a^{2} + b^{2}} = \frac{(a + b)(a - b)}{a^{2} + b^{2}} ＞ 0$，$\frac{a - b}{a + b} ＞ 0$，
$\therefore \frac{a^{2} + b^{2}}{a - b} - \frac{(a + b)^{2}}{a^{2} + b^{2}} = 1 + \frac{a^{2} + b^{2}}{a - b} - 1 = \frac{2ab}{a^{2} + b^{2}} ＞ 1$，$\therefore \frac{a^{2} - b^{2}}{a^{2} + b^{2}} ＞ \frac{a - b}{a + b}$.