2025年绿色通道45分钟课时作业与单元测评高中数学必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年绿色通道45分钟课时作业与单元测评高中数学必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 若把总长为 20 m 的篱笆围成一个矩形场地,则矩形场地的最大面积是 (
A.$ 5\ m^2 $
B.$ 10\ m^2 $
C.$ 20\ m^2 $
D.$ 25\ m^2 $
D
)A.$ 5\ m^2 $
B.$ 10\ m^2 $
C.$ 20\ m^2 $
D.$ 25\ m^2 $
答案:
1.D 设矩形的一边为$x m$,$0<x<10$,则相邻一边为$\frac{1}{2} × (20-2x)=(10-x)m$,设场地面积为$y m^2$,$\therefore y=x(10-x)\leq \left[ \frac{x+(10-x)}{2} \right]^2 =25$,当且仅当$x=10-x$,即$x=5$时等号成立,故$y_{\max}=25$。
2. 某企业 2 月份的产量与 1 月份相比增长率为$ p $,3 月份的产量与 2 月份相比增长率为$ q $($ p>0,q>0 $),若该企业这两个月产量的平均增长率为$ x $,则下列关系中正确的是 (
A.$ x\geqslant \dfrac{p+q}{2} $
B.$ x\leqslant \dfrac{p+q}{2} $
C.$ x>\dfrac{p+q}{2} $
D.$ x<\dfrac{p+q}{2} $
B
)A.$ x\geqslant \dfrac{p+q}{2} $
B.$ x\leqslant \dfrac{p+q}{2} $
C.$ x>\dfrac{p+q}{2} $
D.$ x<\dfrac{p+q}{2} $
答案:
2.B 由题意可得$(1+p)(1+q)=(1+x)^2$,$\therefore (1+x)^2=1+(p+q)+pq\leq 1+(p+q)+\left( \frac{p+q}{2} \right)^2 =\left( \frac{p+q}{2} +1\right)^2$,$\therefore x\leq \frac{p+q}{2}$,当且仅当$p = q$时取等号。
3. 某车间分批生产某种产品,每批的生产准备费用为 900 元,若每批生产$ x $件,则平均仓储时间为$ \dfrac{x}{4} $天,且每件产品每天的仓储费用为 1 元,为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品 (
A.30 件
B.60 件
C.80 件
D.100 件
B
)A.30 件
B.60 件
C.80 件
D.100 件
答案:
3.B 设平均每件产品的生产准备费用与仓储费用之和为$y$元,则$y=\frac{\frac{x}{4} × x × 1+900}{x} =\frac{x}{4} +\frac{900}{x} \geq 2\sqrt{\frac{x}{4} · \frac{900}{x}} =30$,当且仅当$\frac{x}{4} =\frac{900}{x}$,即$x = 60$时等号成立,故每批应生产产品$60$件.故选B.
4. 现设计一个两邻边的长度分别为$ a,b $的矩形广告牌,其面积为$ S $,且$ S = a - b + 5 $,则当该广告牌的周长最小时,$ S = $ (
A.3
B.4
C.5
D.6
A
)A.3
B.4
C.5
D.6
答案:
4.A 由题意知$a>0$,$b>0$,且$ab=a - b+5$,所以$b=\frac{a+5}{a+1}$,则该矩形的周长为$l=2(a+b)=2\left( a+\frac{a+5}{a+1}\right)=2\left( a+1+\frac{4}{a+1}\right)\geq 2× 2\sqrt{(a+1)· \frac{4}{a+1}} =8$,当且仅当$a+1=\frac{4}{a+1}$,即$a=1$,$b=3$时,取得等号,此时$S=ab=3$。
5. (2025·湖南益阳期中)要制作一个容积为$ 8\ m^3 $,高为 2 m 的无盖长方体容器。已知该容器的底面造价是 40 元$ /m^2 $,侧面造价是 20 元$ /m^2 $,则该容器的最低总造价为 (
A.360 元
B.420 元
C.480 元
D.600 元
C
)A.360 元
B.420 元
C.480 元
D.600 元
答案:
5.C 设容器底面长与宽分别为$x m$和$y m$,依题意知,$2xy=8$,即$xy=4$,于是得该容器总造价为$40× 4+20× 4(x+y)=160+80(x+y)\geq 160+80× 2\sqrt{xy}=480$,当且仅当$x=y=2$时取等号,所以该容器的最低总造价为$480$元.
6. (多选)已知某出租车公司为升级服务水平,购入了一批豪华轿车投入运营,据之前的市场分析得出每辆车的运营总利润$ y $(万元)与运营年数$ x $的关系为$ y = -x^2 + 12x - 25 $,则下列判断正确的是 (
A.车辆运营年数越多,利润越高
B.车辆在第 6 年时,总利润最高
C.车辆在前 5 年的平均利润最高
D.车辆每年都能盈利
BC
)A.车辆运营年数越多,利润越高
B.车辆在第 6 年时,总利润最高
C.车辆在前 5 年的平均利润最高
D.车辆每年都能盈利
答案:
6.BC $y=-x^2+12x-25$的图象是开口向下的,故A错误;图象的对称轴为直线$x=6$,故B正确;$\frac{y}{x} =-x+12-\frac{25}{x} =-\left( x+\frac{25}{x} \right)+12\leq -2\sqrt{25}+12=2$,当且仅当$x=5$时,等号成立,故C正确;当$x=1$时,$y=-14$,故D错误.
7. 三国时期赵爽在《勾股方圆图注》中对勾股定理的证明可用现代数学表述为如图所示,则该图对“$ a^2 + b^2 \geqslant 2ab $”的几何解释为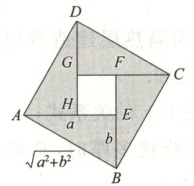
大正方形的面积不小于四个全等直角三角形的面积和,当且仅当$a = b$时等号

答案:
7.大正方形的面积不小于四个全等直角三角形的面积和,当且仅当$a = b$时等号成立
解析 由题图可知,四个直角三角形全等,且它们的直角边长分别为$a$,$b$,斜边长为$\sqrt{a^2+b^2}$,正方形$ABCD$的边长即为$\sqrt{a^2+b^2}$,所以$S_{正方形ABCD}=a^2+b^2$,而四个全等直角三角形的面积和为$4S=4× \frac{1}{2} ab=2ab$,所以$“a^2+b^2\geq 2ab”$的几何解释为大正方形的面积不小于四个全等直角三角形的面积和,当且仅当$a = b$时等号成立.
解析 由题图可知,四个直角三角形全等,且它们的直角边长分别为$a$,$b$,斜边长为$\sqrt{a^2+b^2}$,正方形$ABCD$的边长即为$\sqrt{a^2+b^2}$,所以$S_{正方形ABCD}=a^2+b^2$,而四个全等直角三角形的面积和为$4S=4× \frac{1}{2} ab=2ab$,所以$“a^2+b^2\geq 2ab”$的几何解释为大正方形的面积不小于四个全等直角三角形的面积和,当且仅当$a = b$时等号成立.
8. 为给教室消毒,向室内喷洒某消毒液,已知室内消毒液浓度$ C $(单位:mg/L)随时间$ t $(单位:min)的变化关系为$ C = \dfrac{20t}{t^2 + 25} $,则经过
5
min 后室内消毒液浓度达到最大。
答案:
8.5
解析 由题意可得$t>0$,$C=\frac{20t}{t^2+25} +\frac{20}{t+\frac{25}{t}} \leq \frac{20t}{2\sqrt{t^2× 25}} +\frac{20}{2\sqrt{t× \frac{25}{t}}} =2$,当且仅当$t=\frac{25}{t}$,即$t=5$时取等号.
解析 由题意可得$t>0$,$C=\frac{20t}{t^2+25} +\frac{20}{t+\frac{25}{t}} \leq \frac{20t}{2\sqrt{t^2× 25}} +\frac{20}{2\sqrt{t× \frac{25}{t}}} =2$,当且仅当$t=\frac{25}{t}$,即$t=5$时取等号.
9. 某学校为了支持生物选修课程开展,计划利用学校面积为$ 900\ m^2 $的矩形空地建造试验田,试验田为三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔 1 m,三块矩形区域的前、后与空地边沿各保留 1 m 宽的通道,左、右两块矩形区域分别与相邻的左、右边沿保留 3 m 宽的通道,如图。设矩形空地长为$ x $ m,三块种植植物的矩形区域(如图中阴影部分所示)的总面积为$ S\ m^2 $。
(1)求$ S $关于$ x $的关系式;
(2)求$ S $的最大值及此时$ x $的值。
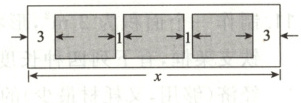
(1)求$ S $关于$ x $的关系式;
(2)求$ S $的最大值及此时$ x $的值。

答案:
9.解
(1)由题知,空地宽为$\frac{900}{x} m$,
则$S=(x - 8)× \left( \frac{900}{x} -2\right)=916 - 2x - \frac{7200}{x}(8<x<450)$.
(2)由
(1)知,$S=916 - 2x - \frac{7200}{x}(8<x<450)$,
因为$2x+\frac{7200}{x} \geq 2\sqrt{2x· \frac{7200}{x}} =240$,
当且仅当$2x=\frac{7200}{x}$,即$x=60$时,等号成立,
故$S\leq 676$,
故$S$的最大值为$676$,此时$x$的值为$60$.
(1)由题知,空地宽为$\frac{900}{x} m$,
则$S=(x - 8)× \left( \frac{900}{x} -2\right)=916 - 2x - \frac{7200}{x}(8<x<450)$.
(2)由
(1)知,$S=916 - 2x - \frac{7200}{x}(8<x<450)$,
因为$2x+\frac{7200}{x} \geq 2\sqrt{2x· \frac{7200}{x}} =240$,
当且仅当$2x=\frac{7200}{x}$,即$x=60$时,等号成立,
故$S\leq 676$,
故$S$的最大值为$676$,此时$x$的值为$60$.
查看更多完整答案,请扫码查看


