《2025年名师面对面满分特训方案九年级数学全一册人教版台州专版》

11.若$\triangle ABC$的每条边长增加各自的10%得$\triangle A'B'C'$,则$\angle B'的度数与其对应角\angle B$的度数相比 ( )

A.增加了10%
B.减少了10%
C.增加了$(1+10\%)$
D.没有改变

答案： D

12.下面四个图案：不等边三角形、等边三角形、正方形和矩形,其中每个图案花边的宽度都相同,那么每个图形中花边的内外边缘所围成的几何图形不相似的个数有 ( )


A.4个
B.3个
C.2个
D.1个

答案： D

13.已知$\frac{x}{2}= \frac{y}{3}= \frac{z}{4}$,则$\frac{x^2+xy}{yz}= $______.

答案： $\frac{5}{6}$

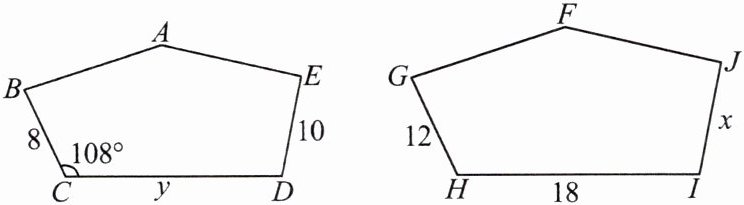
14.如图,五边形ABCDE和五边形FGHIJ相似,求图中未知的边长x,y和$\angle H$的大小.

答案： 解:
∵五边形ABCDE和五边形FGHIJ相似,
∴∠H=∠C=108°, $\frac{BC}{GH}$=$\frac{CD}{HI}$=$\frac{DE}{IJ}$,即$\frac{8}{12}$=$\frac{y}{18}$=$\frac{10}{x}$,解得x=15,y=12.

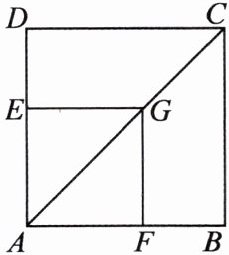
15.如图,G是正方形ABCD对角线AC上一点,作$GE\perp AD$,$GF\perp AB$,垂足分别为E,F.求证：四边形AFGE与正方形ABCD相似.

答案： 解:
∵四边形ABCD是正方形,AC是对角线,
∴∠DAC=∠BAC=45°.又
∵GE⊥AD,GF⊥AB,
∴EG=FG,且AE=EG,AF=FG,
∴AE=EG=FG=AF,即四边形AFGE为正方形.
∴$\frac{AF}{AB}$=$\frac{FG}{BC}$=$\frac{GE}{CD}$=$\frac{AE}{AD}$,且∠EAF=∠DAB,∠AFG=∠ABC,∠FGE=∠BCD,∠AEG=∠ADC.
∴四边形AFGE与正方形ABCD相似.

16.在$AB= 30\ m$,$AD= 20\ m$的矩形花坛四周修筑小路.
(1)如图1,如果四周的小路的宽均相等,那么小路四周所围成的矩形$A'B'C'D'$和矩形ABCD相似吗？请说明理由.
(2)如图2,如果相对着的两条小路的宽均相等,试问小路的宽x与y的比值为多少时,能使小路四周所围成的矩形$A'B'C'D'$和矩形ABCD相似？请说明理由.

答案： 解:
(1)如果四周的小路的宽均相等,那么小路四周所围成的矩形A'B'C'D'和矩形ABCD不相似;设四周的小路的宽为x,
∴$\frac{30+2x}{30}$=$\frac{15+x}{15}$,$\frac{20+2x}{20}$=$\frac{10+x}{10}$,
∴$\frac{30+2x}{30}$≠$\frac{20+2x}{20}$,
∴小路四周所围成的矩形A'B'C'D'和矩形ABCD不相似.
(2)
∵当$\frac{30+2y}{30}$=$\frac{20+2x}{20}$时,小路四周所围成的矩形A'B'C'D'和矩形ABCD相似,解得$\frac{x}{y}$=$\frac{2}{3}$,
∴小路的宽x与y的比值为2:3时,能使小路四周所围成的矩形A'B'C'D'和矩形ABCD相似.