第55页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
10.不透明袋中装有除颜色外完全相同的a个白球、b个红球,则任意摸出一个球是红球的概率是 ( )
A.$\frac{b}{a+b}$
B.$\frac{b}{a}$
C.$\frac{a}{a+b}$
D.$\frac{a}{b}$
A.$\frac{b}{a+b}$
B.$\frac{b}{a}$
C.$\frac{a}{a+b}$
D.$\frac{a}{b}$
答案:
A
11.如图,正方形ABCD及其内切圆O,随机地往正方形内投一粒米,落在阴影部分的概率是 ( )
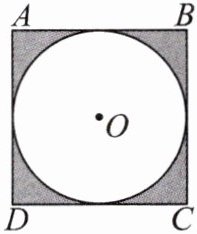
A.$\frac{\pi}{4}$
B.$1-\frac{\pi}{4}$
C.$\frac{\pi}{8}$
D.$1-\frac{\pi}{9}$

A.$\frac{\pi}{4}$
B.$1-\frac{\pi}{4}$
C.$\frac{\pi}{8}$
D.$1-\frac{\pi}{9}$
答案:
B
12.一个十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒.当你抬头看信号灯时,是绿灯的概率是______.
答案:
$\frac{5}{12}$
13.在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格:
|事件A|必然事件|随机事件|
|m的值|______|______|

(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于$\frac{4}{5}$,求m的值.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格:
|事件A|必然事件|随机事件|
|m的值|______|______|

(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于$\frac{4}{5}$,求m的值.
答案:
4 2 或 3 解:
(1)当袋子中全为黑球,即取出 4 个红球后,摸到黑球是必然事件;当取出 2 个或 3 个红球时,摸到黑球为随机事件.
(2)根据题意,得$\frac{m+6}{4+6}=\frac{4}{5}$,解得$m=2$,所以 m 的值为 2.
(1)当袋子中全为黑球,即取出 4 个红球后,摸到黑球是必然事件;当取出 2 个或 3 个红球时,摸到黑球为随机事件.
(2)根据题意,得$\frac{m+6}{4+6}=\frac{4}{5}$,解得$m=2$,所以 m 的值为 2.
14.某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
(1)求转动一次转盘获得购物券的概率.
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更划算?
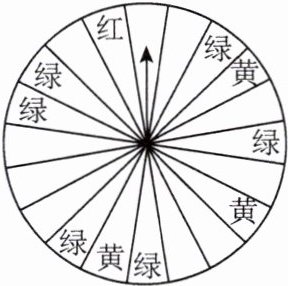
(1)求转动一次转盘获得购物券的概率.
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更划算?

答案:
解:
(1)
∵转盘被均匀分为 20 份,转动一次转盘获得购物券的有 10 种情况,
$\therefore P_{(转动一次转盘获得购物券)}=\frac{10}{20}=\frac{1}{2}$.
(2)$\because P_{(红色)}=\frac{1}{20}$,$P_{(黄色)}=\frac{3}{20}$,$P_{(绿色)}=\frac{6}{20}=\frac{3}{10}$,
$\therefore 200×\frac{1}{20}+100×\frac{3}{20}+50×\frac{6}{20}=40$(元)
∵40 元>30 元,
∴选择转转盘对顾客更划算.
(1)
∵转盘被均匀分为 20 份,转动一次转盘获得购物券的有 10 种情况,
$\therefore P_{(转动一次转盘获得购物券)}=\frac{10}{20}=\frac{1}{2}$.
(2)$\because P_{(红色)}=\frac{1}{20}$,$P_{(黄色)}=\frac{3}{20}$,$P_{(绿色)}=\frac{6}{20}=\frac{3}{10}$,
$\therefore 200×\frac{1}{20}+100×\frac{3}{20}+50×\frac{6}{20}=40$(元)
∵40 元>30 元,
∴选择转转盘对顾客更划算.
查看更多完整答案,请扫码查看


