《2025年名师面对面满分特训方案九年级数学全一册人教版台州专版》

1.如图,AB 是$\odot O$的直径,点 E,C 在$\odot O$上,点 A 是$\widehat {EC}$的中点,过点 A 画$\odot O$的切线,交 BC 的延长线于点 D,连接 EC.若$∠ADB= 58.5^{\circ }$,则$∠ACE$的度数为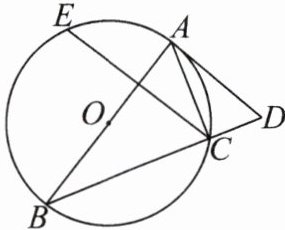
( )

A.$29.5^{\circ }$
B.$31.5^{\circ }$
C.$58.5^{\circ }$
D.$63^{\circ }$

答案： B

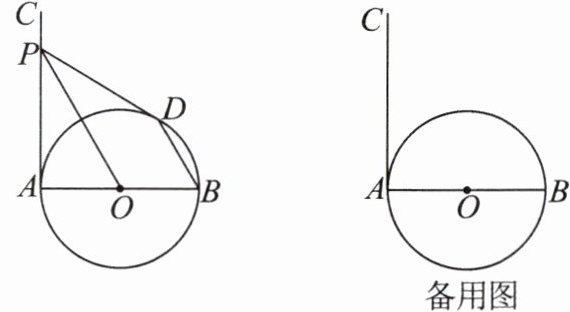
2.如图,AB 是$\odot O$的直径,过点 A 作$\odot O$的切线 AC,点 P 是射线 AC 上的动点,连接 OP,过点 B 作$BD// OP$,交$\odot O$于点 D,连接 PD.
(1)求证:PD 是$\odot O$的切线.
(2)当四边形 POBD 是平行四边形时,求$∠APO$的度数.

答案：
(1)证明:连接OD,
∵PA切⊙O于A,
∴PA⊥AB,即∠PAO =90°.
∵OP//BD,
∴∠DBO=∠AOP,∠BDO=∠DOP.
∵OD=OB,
∴∠BDO=∠DBO,
∴∠DOP=∠AOP.
在△AOP和△DOP中，$\begin{cases}AO = DO\\∠AOP = ∠DOP\\PO = PO\end{cases}$
∴△AOP≌△DOP(SAS),
∴∠PDO=∠PAO=90°,即OD ⊥PD,
∵OD过点O,
∴PD是⊙O的切线
(2)解:由
(1)知△AOP≌△DOP,
∴PA=PD.
∵四边形POBD是平行四边形，
∴PD=OB,
∵OB=OA,
∴PA=OA,
∴∠APO=∠AOP,
∵∠PAO=90°,
∴∠APO=∠AOP = 45°.

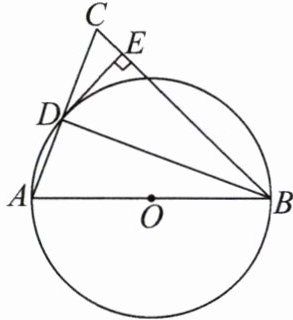
3.如图,在$\triangle ABC$中,$BA= BC$,以 AB 为直径作$\odot O$,交 AC 于点 D,连接 DB,过点 D 作$DE⊥BC$,垂足为 E.
(1)求证:DE 为$\odot O$的切线.
(2)若$∠C= 60^{\circ },DE= \sqrt {3}$,求 AD 的长.

答案：

(1)证明:连接OD,如图.
∵AB为直径，
∴∠ADB=90°.
∵BA=BC,
∴AD=CD.
∵AO=OB,
∴OD为△BAC的中位线，
∴OD//BC.
∵DE⊥BC,
∴∠ODE=∠BED=90°,
∴OD⊥DE,
∵OD是⊙O的半径，
∴DE为⊙O的切线

(2)解:在Rt△CDE中,∠C=60°,DE=$\sqrt{3}$,
∴∠CDE=30°,
∴CD=2.
∵AB为⊙O的直径，
∴BD⊥AC,
∵BA=BC,
∴AD=CD=2.

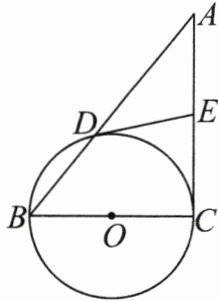
4.如图,在$Rt\triangle ABC$中,$∠C= 90^{\circ }$,以 BC 为直径的$\odot O$交 AB 于点 D,切线 DE 交 AC 于点 E.
(1)求证:$∠A= ∠ADE.$
(2)若$AD= 16,DE= 10$,求 BC 的长.

答案：

(1)证明:连接OD,
∵DE是切线，
∴∠ODE=90°,
∴∠ADE+∠BDO=90°.
∵∠ACB=90°,
∴∠A+∠B=90°,
∵OD=OB,
∴∠B=∠BDO,
∴∠ADE=∠A.

(2)连接CD.
∵∠ADE=∠A,
∴AE=DE.
∵BC是⊙O的直径,∠ACB=90°,
∴EC是⊙O的切线，
∴ED=EC,
∴AE=EC.
∵DE=10,
∴AC=2DE=20.
在Rt△ADC中,DC=$\sqrt{20^{2}-16^{2}}$=12.
设BD=x,在Rt△BDC中,BC²=x²+12²,
在Rt△ABC中,BC²=(x+16)²−20²,
∴x²+12²=(x+16)²−20²,解得x=9,
∴BC=$\sqrt{12^{2}+9^{2}}$=15.