第38页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1.下列说法正确的是 ( )
A.平分弦的直径垂直于弦
B.垂直于弦的直线必过圆心
C.垂直于弦的直径平分弦
D.平分弦的直径平分弦所对的弧
A.平分弦的直径垂直于弦
B.垂直于弦的直线必过圆心
C.垂直于弦的直径平分弦
D.平分弦的直径平分弦所对的弧
答案:
C
2.如图,已知⊙O 的直径AB⊥CD 于点E,则下列结论错误的是 ( )
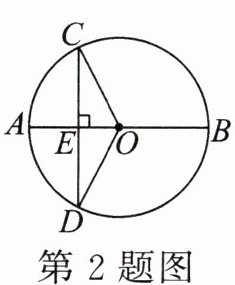
A.CE= DE
B.AE= OE
C.$\widehat{BC}= \widehat{BD}$
D.△OCE≌△ODE

A.CE= DE
B.AE= OE
C.$\widehat{BC}= \widehat{BD}$
D.△OCE≌△ODE
答案:
B
3.已知⊙O 的半径为7,AB 是⊙O 的弦,点 P 在弦AB 上.若PA= 4,PB= 6,则 OP= ( )
A.$\sqrt{14}$
B.4
C.$\sqrt{23}$
D.5
A.$\sqrt{14}$
B.4
C.$\sqrt{23}$
D.5
答案:
D
4.如图,在5×5 正方形网格中,一条圆弧经过A,B,C 三点,已知点A 的坐标是(-2,4),点C 的坐标是(1,3),则这条圆弧所在圆的圆心坐标是 ( )
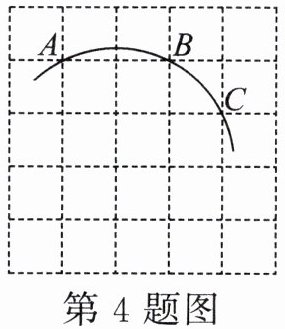
A.(0,0)
B.(-1,2)
C.(-1,0)
D.(-1,-1)

A.(0,0)
B.(-1,2)
C.(-1,0)
D.(-1,-1)
答案:
B
5.如图,A,B,C 是⊙O 上的点,OC⊥AB,垂足为点 D,且 D 为 OC 的中点.若 OA= 7,则 BC的长为______.
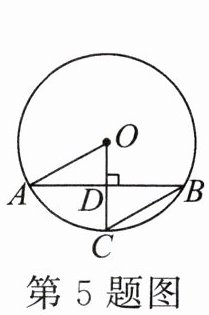

答案:
7
6.如图,△ABC 中,AB= 4,AC= 5,BC= 2,以A 为圆心,AC 长为半径作圆A,延长 CB 交圆A 于点 D,则 BD 的长为______.
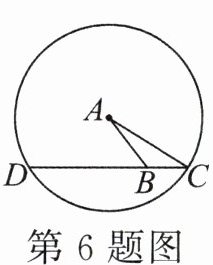

答案:
$\frac{9}{2}$
7.如图是一个隧道的横截面,它的形状是以点 O为圆心的圆的一部分,如果 C 是⊙O 中弦AB的中点,CD 经过圆心 O 交⊙O 于点 D,并且AB= 4m,CD= 6m,则⊙O 的半径长为______m.
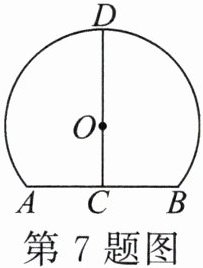

答案:
$\frac{10}{3}$
8.石拱桥是我国古代人民勤劳和智慧的结晶(如图1),隋代建造的赵州桥距今约有1400年历史,是我国古代石拱桥的代表.如图2 是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为$\widehat{AB}$.桥的跨度(弧所对的弦长)AB= 26m,设$\widehat{AB}$所在圆的圆心为 O,半径 OC⊥AB,垂足为 D.拱高(弧的中点到弦的距离)CD= 5m.连接 OB.
(1)直接判断 AD 与 BD 的数量关系.
(2)求这座石拱桥主桥拱的半径(精确到1m).
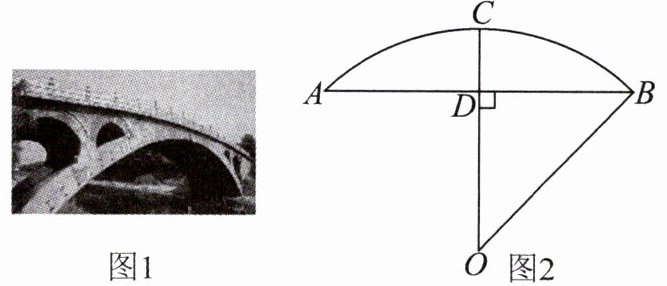
(1)直接判断 AD 与 BD 的数量关系.
(2)求这座石拱桥主桥拱的半径(精确到1m).

答案:
解:
(1)
∵OC⊥AB,
∴AD=BD.
(2)设主桥拱半径为R,由题意可知AB=26,CD=5,
∴BD=$\frac{1}{2}$AB=13,OD=OC−CD=R−5,
∵∠ODB=90°,
∴OD²+BD²=OB²,
∴(R−5)²+13²=R²,解得R=19.4≈19,
答:这座石拱桥主桥拱的半径约为19m.
(1)
∵OC⊥AB,
∴AD=BD.
(2)设主桥拱半径为R,由题意可知AB=26,CD=5,
∴BD=$\frac{1}{2}$AB=13,OD=OC−CD=R−5,
∵∠ODB=90°,
∴OD²+BD²=OB²,
∴(R−5)²+13²=R²,解得R=19.4≈19,
答:这座石拱桥主桥拱的半径约为19m.
查看更多完整答案,请扫码查看


