第48页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1.如图,四边形ABCD是⊙O的内接四边形,∠B= 58°,∠ACD= 40°.若⊙O的半径为5,则$\widehat{DC}$的长为( )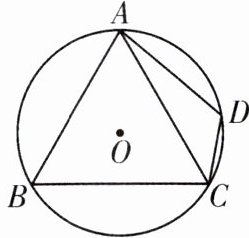
A.$\frac{13}{3}\pi$
B.$\frac{10}{9}\pi$
C.$\pi$
D.$\frac{1}{2}\pi$

A.$\frac{13}{3}\pi$
B.$\frac{10}{9}\pi$
C.$\pi$
D.$\frac{1}{2}\pi$
答案:
C
2.一条弧所对的圆心角为135°,弧长等于半径为3 cm的圆的周长的5倍,则这条弧的半径为( )
A.45 cm
B.40 cm
C.35 cm
D.30 cm
A.45 cm
B.40 cm
C.35 cm
D.30 cm
答案:
B
3.如图,在边长为2的等边△ABC中,D是BC边上的中点,以点A为圆心,AD为半径作圆与AB,AC分别交于E,F两点,则图中阴影部分的面积为( )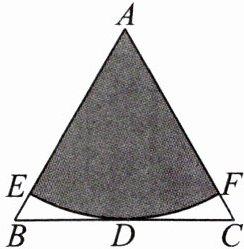
A.$\frac{\pi}{6}$
B.$\frac{\pi}{3}$
C.$\frac{\pi}{2}$
D.$\frac{2\pi}{3}$

A.$\frac{\pi}{6}$
B.$\frac{\pi}{3}$
C.$\frac{\pi}{2}$
D.$\frac{2\pi}{3}$
答案:
C
4.一个垃圾填埋场,它在地面上的形状为长80 m,宽60 m的矩形,有污水从该矩形的四周边界向外渗透了3 m,则该垃圾填埋场外围受污染土地的面积为( )
A.$(840+6\pi)\ m^2$
B.$(840+9\pi)\ m^2$
C.$840\ m^2$
D.$876\ m^2$
A.$(840+6\pi)\ m^2$
B.$(840+9\pi)\ m^2$
C.$840\ m^2$
D.$876\ m^2$
答案:
B
5.如图,边长为4的正方形ABCD内接于⊙O,则$\widehat{AB}$的长是______(结果保留π).[img]
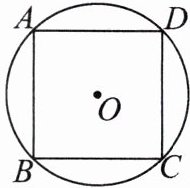

答案:
$\sqrt{2}\pi$
6.如图,$\widehat{AB}$的半径OA= 2,OC⊥AB于点C,∠AOC= 60°.
(1)求弦AB的长.
(2)求$\widehat{AB}$的长.
(1)求弦AB的长.
(2)求$\widehat{AB}$的长.

答案:
解:
(1)
∵$\overset{\frown}{AB}$的半径$OA = 2$,$OC⊥AB$于点$C$,$\angle AOC = 60^{\circ}$,
∴$AC = \sqrt{3}$,$\therefore AB = 2AC = 2\sqrt{3}$.
(2)
∵$OC⊥AB$,$\angle AOC = 60^{\circ}$,$\therefore\angle AOB = 120^{\circ}$,$\because OA = 2$,
∴$\overset{\frown}{AB}$的长是$\frac{120×\pi×2}{180}=\frac{4\pi}{3}$.
(1)
∵$\overset{\frown}{AB}$的半径$OA = 2$,$OC⊥AB$于点$C$,$\angle AOC = 60^{\circ}$,
∴$AC = \sqrt{3}$,$\therefore AB = 2AC = 2\sqrt{3}$.
(2)
∵$OC⊥AB$,$\angle AOC = 60^{\circ}$,$\therefore\angle AOB = 120^{\circ}$,$\because OA = 2$,
∴$\overset{\frown}{AB}$的长是$\frac{120×\pi×2}{180}=\frac{4\pi}{3}$.
7.如图,C,D是以AB为直径的半圆上的两点,∠CAB= ∠DBA,连接BC,CD.
(1)求证:CD//AB.
(2)若AB= 4,∠ACD= 30°,求阴影部分的面积.
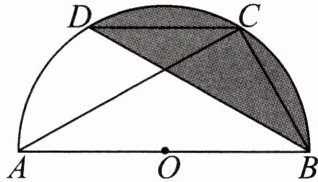
(1)求证:CD//AB.
(2)若AB= 4,∠ACD= 30°,求阴影部分的面积.

答案:
(1)证明:
∵$\overset{\frown}{AD}=\overset{\frown}{AD}$,
∴$\angle ACD = \angle DBA$.
又
∵$\angle CAB = \angle DBA$,
∴$\angle CAB = \angle ACD$,$\therefore CD// AB$.

(2)如图,连接$OD$,过点$D$作$DE⊥AB$,垂足为$E$.
∵$\angle ACD = 30^{\circ}$,$\therefore\angle AOD = 60^{\circ}$,$\therefore\angle BOD = 180^{\circ}-\angle AOD = 120^{\circ}$,$\therefore S_{扇形BOD}=\frac{n\pi r^{2}}{360}=\frac{120×\pi×2^{2}}{360}=\frac{4}{3}\pi$.在$Rt\triangle ODE$中,
可得$DE = \sqrt{3}$,$\therefore S_{\triangle BOD}=\frac{1}{2}OB\cdot DE=\frac{1}{2}×2×\sqrt{3}=\sqrt{3}$,
$\therefore S_{阴影}=S_{扇形BOD}-S_{\triangle BOD}=\frac{4}{3}\pi-\sqrt{3}$.
(1)证明:
∵$\overset{\frown}{AD}=\overset{\frown}{AD}$,
∴$\angle ACD = \angle DBA$.
又
∵$\angle CAB = \angle DBA$,
∴$\angle CAB = \angle ACD$,$\therefore CD// AB$.

(2)如图,连接$OD$,过点$D$作$DE⊥AB$,垂足为$E$.
∵$\angle ACD = 30^{\circ}$,$\therefore\angle AOD = 60^{\circ}$,$\therefore\angle BOD = 180^{\circ}-\angle AOD = 120^{\circ}$,$\therefore S_{扇形BOD}=\frac{n\pi r^{2}}{360}=\frac{120×\pi×2^{2}}{360}=\frac{4}{3}\pi$.在$Rt\triangle ODE$中,
可得$DE = \sqrt{3}$,$\therefore S_{\triangle BOD}=\frac{1}{2}OB\cdot DE=\frac{1}{2}×2×\sqrt{3}=\sqrt{3}$,
$\therefore S_{阴影}=S_{扇形BOD}-S_{\triangle BOD}=\frac{4}{3}\pi-\sqrt{3}$.
查看更多完整答案,请扫码查看


