《2025年名师面对面满分特训方案九年级数学全一册人教版台州专版》

10.下列函数中,二次函数有 ( )
①y= 1-$\sqrt{2}$x^2;②y= $\frac{1}{x^2}$;③y= x(1-x);④y= (1-2x)(1+2x);⑤y= 9x^2-(3x-1)^2.

A.1个
B.2个
C.3个
D.4个

答案： C

11.有长24 m的篱笆,一面利用围墙围成如图中间隔有一道篱笆的矩形花圃,设花圃垂直于墙的一边长为x m,面积是$S m^2,$则S与x之间的关系式是 ( )
$A.S= -3x^2+24x$
$B.S= -2x^2-24x$
$C.S= -3x^2-24x$
$D.S= -2x^2+24x$

答案： A

12.已知函数$y= (m+3)x^{m^2-7}.$
(1)当m为何值时,此函数是正比例函数?
(2)当m为何值时,此函数是二次函数?

答案： 解:
(1)因为函数y=(m+3)x^{m²-7}是正比例函数,所以m²-7=1且m+3≠0,解得m₁=-2√2,m₂=2√2,所以当m=±2√2时,此函数是正比例函数.
(2)因为函数y=(m+3)x^{m²-7}是二次函数,所以m²-7=2且m+3≠0,解得m=3,所以当m=3时,此函数是二次函数.

13.一辆汽车的行驶距离s(m)与行驶时间t(s)的函数关系式是s= 9t+$\frac{1}{2}$t^2,经12 s汽车行驶了多远？行驶380 m需要多少时间？

答案： 解:当t=12时,s=9×12+1/2×12²=180.
∴经12 s汽车行驶了180 m.当s=380时,9t+1/2t²=380.解得t₁=20,t₂=-38(不合题意,舍去).
∴该汽车行驶380 m需要20 s.

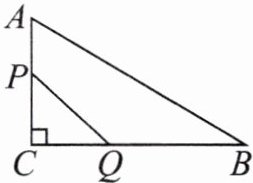
14.如图,在Rt△ABC中,∠C= 90°,AC= 12 mm,BC= 24 mm,动点P从点A开始沿边AC向C以2 mm/s的速度移动,动点Q从点C开始沿边CB向B以4 mm/s的速度移动.如果P,Q两点同时出发,请写出△PCQ的面积S与出发时间t之间的函数关系式及t的取值范围.

答案： 解:依题意,得PC=12-2t,CQ=4t,
∴S=1/2×(12-2t)×4t=-4t²+24t.
∵t＞0,12-2t＞0,
∴0＜t＜6.
∴s=-4t²+24t(0＜t＜6).

15.某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.设每个房间每天的定价增加x元.求：
(1)房间每天的入住量y(间)关于x(元)的函数关系式.
(2)该宾馆每天的收入z(元)关于x(元)的函数关系式.
(3)该宾馆每天的收入能否达到15 000元？若能,请求出此时每个房间的定价；若不能,请说明理由.

答案： 解:
(1)依题意,得y=-x/10+60.
(2)由题意,得z=(200+x)(-x/10+60),即z=-x²/10+40x+12 000.
(3)该宾馆每天的收入能达到15 000元.理由如下:由题意,得z=15 000,即-x²/10+40x+12 000=15 000,解得x₁=100,x₂=300.
∴此时每个房间的定价为300元或500元.