第37页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
8.如图,在4×4的网格纸中,△ABC的三个顶点都在格点上.现要在这张网格纸的四个格点M,N,P,Q中找一点作为旋转中心,将△ABC绕着这个中心进行旋转,旋转前后的两个三角形成中心对称,且旋转后的三角形的三个顶点都在这张4×4的网格纸的格点上,那么满足条件的旋转中心有( )
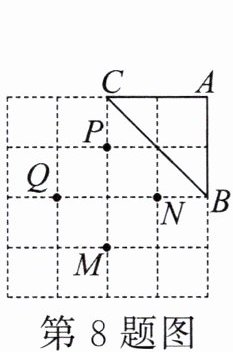
A.点M,点N
B.点M,点Q
C.点N,点P
D.点P,点Q

A.点M,点N
B.点M,点Q
C.点N,点P
D.点P,点Q
答案:
C
9.如图,在Rt△ABC中,∠ABC= 90°,∠ACB= 30°.将△ABC绕点C顺时针旋转60°得到△DEC,点A,B的对应点分别是D,E,点F是边AC的中点,连接BF,BE,FD,则下列结论错误的是( )
A.BE= BC
B.BF//DE,BF= DE
C.∠DFC= 90°
D.DG= 3GF
A.BE= BC
B.BF//DE,BF= DE
C.∠DFC= 90°
D.DG= 3GF
答案:
D
10.如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB= 60°,对角线AC所在的直线绕点O顺时针旋转角α(0°<α<120°),所得的直线l分别交AD,BC于点E,F.
(1)求证:△AOE≌△COF.
(2)当旋转角α为多少度时,四边形AFCE为菱形?试说明理由.
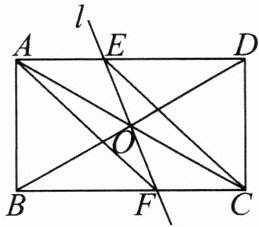
(1)求证:△AOE≌△COF.
(2)当旋转角α为多少度时,四边形AFCE为菱形?试说明理由.

答案:
(1)证明:
∵四边形ABCD是矩形,
∴AD//BC,AO=CO,
∴∠AEO=∠CFO.
在△AOE和△COF中,
$\left\{\begin{array}{l} ∠AEO=∠CFO,\\ ∠AOE=∠COF,\\ AO=CO,\end{array}\right. $
∴△AOE≌△COF(AAS).
(2)当α=90°时,四边形AFCE为菱形.理由:
∵△AOE≌△COF,
∴OE=OF.又
∵AO=CO,
∴四边形AFCE为平行四边形.又
∵∠AOE=90°,
∴四边形AFCE为菱形.
(1)证明:
∵四边形ABCD是矩形,
∴AD//BC,AO=CO,
∴∠AEO=∠CFO.
在△AOE和△COF中,
$\left\{\begin{array}{l} ∠AEO=∠CFO,\\ ∠AOE=∠COF,\\ AO=CO,\end{array}\right. $
∴△AOE≌△COF(AAS).
(2)当α=90°时,四边形AFCE为菱形.理由:
∵△AOE≌△COF,
∴OE=OF.又
∵AO=CO,
∴四边形AFCE为平行四边形.又
∵∠AOE=90°,
∴四边形AFCE为菱形.
11.△ABC和△ADE都是等边三角形.当△ADE绕点A旋转到图1的位置时,连接BD,CE相交于点P,连接PA.
(1)请猜想线段PA,PB,PC之间的数量关系,并加以证明.
(2)将△ADE绕点A旋转到图2的位置时,其他条件不变,请直接写出线段PA,PB,PC之间的数量关系,不需要证明.
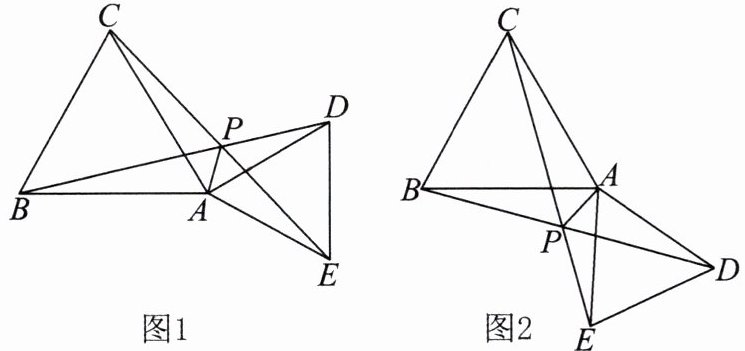
(1)请猜想线段PA,PB,PC之间的数量关系,并加以证明.
(2)将△ADE绕点A旋转到图2的位置时,其他条件不变,请直接写出线段PA,PB,PC之间的数量关系,不需要证明.

答案:
(1)PB=PA+PC,理由如下:如图1,在BP上截取BF =PC,连接AF,
∵△ABC、△ADE都是等边三角形,
∴AB =AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠CAD+∠DAE,即∠DAB=∠EAC,
∴△ABD ≌△ACE(SAS),
∴∠ABD=∠ACE.
∵AB=AC,BF=CP,
∴△BAF≌△CAP(SAS),
∴AF=AP,∠BAF=∠CAP,
∴∠BAC=∠PAF=60°,
∴△AFP是等边三角形,
∴PF=PA,
∴PB=BF+PF=PC+PA.

(2)PC=PA+PB,理由如下:如图2,在PC上截取CM=PB,连接AM,同理得:△ABD≌△ACE(SAS),
∴∠ABD=∠ACE.
∵AB=AC,PB=CM,
∴△AMC≌△APB(SAS),
∴AM=AP、∠BAP=∠CAM,
∴∠BAC=∠PAM=60°,
∴△AMP是等边三角形,
∴PM=PA,
∴PC=PM+CM=PA+PB.

(1)PB=PA+PC,理由如下:如图1,在BP上截取BF =PC,连接AF,
∵△ABC、△ADE都是等边三角形,
∴AB =AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠CAD+∠DAE,即∠DAB=∠EAC,
∴△ABD ≌△ACE(SAS),
∴∠ABD=∠ACE.
∵AB=AC,BF=CP,
∴△BAF≌△CAP(SAS),
∴AF=AP,∠BAF=∠CAP,
∴∠BAC=∠PAF=60°,
∴△AFP是等边三角形,
∴PF=PA,
∴PB=BF+PF=PC+PA.

(2)PC=PA+PB,理由如下:如图2,在PC上截取CM=PB,连接AM,同理得:△ABD≌△ACE(SAS),
∴∠ABD=∠ACE.
∵AB=AC,PB=CM,
∴△AMC≌△APB(SAS),
∴AM=AP、∠BAP=∠CAM,
∴∠BAC=∠PAM=60°,
∴△AMP是等边三角形,
∴PM=PA,
∴PC=PM+CM=PA+PB.

查看更多完整答案,请扫码查看


