《2025年名师面对面满分特训方案九年级数学全一册人教版台州专版》

1.抛物线 $y= ax^{2}+bx+c$ 上部分点的横坐标$x$,纵坐标$y$的对应值如下表：
| x | -2 | -1 | 0 | 1 |
| y | 0 | 4 | 6 | 6 |
下列结论不正确的是 ( )

A.抛物线的开口向下
B.抛物线的对称轴为直线$x= \frac{1}{2}$
C.抛物线与x轴的一个交点坐标为$(2,0)$
D.函数$y= ax^{2}+bx+c的最大值为\frac{25}{4}$

答案： C

2.已知点$A(4,y_{1}),B(\sqrt{2},y_{2}),C(-2,y_{3})都在二次函数y= (x-2)^{2}-1$的图象上,则$y_{1}$,$y_{2}$,$y_{3}$的大小关系是______.

答案： y₃＞y₁＞y₂

3.如图,已知二次函数$y= x^{2}+ax+3的图象经过点P(-2,3)$.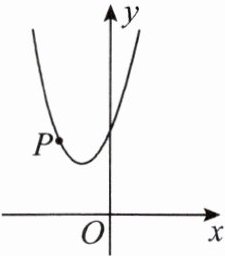
(1)求$a$的值和图象的顶点坐标.
(2)点$Q(m,n)$在该二次函数图象上.
①当$m= 2$时,求$n$的值；
②若点$Q到y$轴的距离小于2,请根据图象直接写出$n$的取值范围.

答案： 解:
(1)将(-2,3)代入y=x²+ax+3得到a=2,
∴y=x²+2x+3=(x+1)²+2,
∴顶点坐标为(-1,2).
(2)①当m=2时,n=11;②
∵点Q到y轴的距离小于2,
∴|m|＜2,
∴-2＜m＜2,
∴2≤n＜11.

4.若二次函数的图象的顶点坐标为$(2,-1)$,且抛物线过$(0,3)$,则二次函数的解析式是 ( )

A.$y= -(x-2)^{2}-1$
B.$y= -\frac{1}{2}(x-2)^{2}-1$
C.$y= (x-2)^{2}-1$
D.$y= \frac{1}{2}(x-2)^{2}-1$

答案： C

5.已知抛物线$y= ax^{2}+bx+c经过A(-3,0)$,$B(1,0)$,$C(0,3)$,则该抛物线的解析式为______.

答案： y=-x²-2x+3

6.二次函数$y= \frac{3}{4}x^{2}+bx+c$,其图象对称轴为直线$x= 1$,且经过点$(2,-\frac{9}{4})$.求此二次函数的表达式.

答案： 解:由已知条件得$\left\{\begin{array}{l} -\frac {b}{2× \frac {3}{4}}=1,\\ \frac {3}{4}× 2^{2}+2b+c=-\frac {9}{4},\end{array}\right. $解得$\left\{\begin{array}{l} b=-\frac {3}{2},\\ c=-\frac {9}{4},\end{array}\right. $$\therefore$此二次函数的表达式为$y=\frac {3}{4}x^{2}-\frac {3}{2}x-\frac {9}{4}$.

7.已知抛物线$y= x^{2}+mx的对称轴为直线x= 2$,则关于$x的方程x^{2}+mx= 5$的根是( )

A.0,4
B.1,5
C.1,-5
D.-1,5

答案： D

8.已知$y= ax^{2}+bx+c(a≠0)$的图象如图所示,对称轴为直线$x= 2$.若$x_{1}$,$x_{2}是一元二次方程ax^{2}+bx+c= 0(a≠0)$的两个根,且$x_{1}＜x_{2}$,$-1＜x_{1}＜0$,则下列说法正确的是 ( )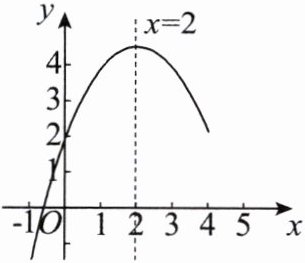

A.$x_{1}+x_{2}＜0$
B.$4＜x_{2}＜5$
C.$b^{2}-4ac＜0$
D.$ab＞0$

答案： B