《2025年名师面对面满分特训方案九年级数学全一册人教版台州专版》

1.下列说法正确的是 ( )

A.任意两个菱形都相似
B.任意两个矩形都相似
C.任意两个等腰三角形都相似
D.任意两个正方形都相似

答案： D

2.下列图形中,不是相似图形的一组是 ( )

答案： D

3.下列线段中,能成比例的是 ( )

A.3 cm,6 cm,8 cm,9 cm
B.3 cm,5 cm,6 cm,9 cm
C.3 cm,6 cm,7 cm,9 cm
D.3 cm,6 cm,9 cm,18 cm

答案： D

4.已知$\frac{a}{b}= \frac{2}{5}$,则$\frac{a+b}{b}$的值为 ( )

A.$\frac{2}{5}$
B.$\frac{3}{5}$
C.$\frac{2}{3}$
D.$\frac{7}{5}$

答案： D

5.在比例尺为1:2000的地图上测得A,B两地间的图上距离为5 cm,则A,B两地间的实际距离为 ( )

A.10 m
B.25 m
C.100 m
D.10000 m

答案： C

6.如图,若两个四边形相似,则$\angle\alpha$的度数是 ( )


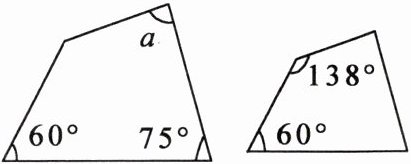
A.$75^\circ$
B.$60^\circ$
C.$87^\circ$
D.$120^\circ$

答案： C

7.一个四边形的各边之比为1:2:3:4,和它相似的另一个四边形的最小边长为5 cm,则它的最大边长为 ( )

A.10 cm
B.15 cm
C.20 cm
D.25 cm

答案： C

8.如图,正五边形FGHMN与正五边形ABCDE相似.若$AB:FG= 2:3$,则下列结论正确的是 ( )


A.$2DE= 3MN$
B.$3DE= 2MN$
C.$3\angle A= 2\angle F$
D.$2\angle A= 3\angle F$

答案： B

9.已知a,b,d,c是成比例线段,$a= 4\ cm$,$b= 6\ cm$,$d= 9\ cm$,则$c= $______.

答案： 13.5 cm

10.如图,$\triangle ABC$中,D,E分别为边AB,AC的中点.
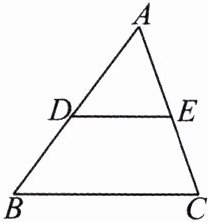
(1)证明：$\triangle ADE与\triangle ABC$相似.
(2)求$\triangle ADE与\triangle ABC$的相似比.

答案：
(1)证明:
∵在△ABC中,点D,点E分别是线段AB,AC的中点,
∴DE是△ABC的中位线,
∴DE//BC且DE=$\frac{1}{2}$BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE与△ABC相似.
(2)解:
∵△ADE∽△ABC,
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{DE}{BC}$=$\frac{1}{2}$,
∴△ADE与△ABC的相似比为$\frac{AD}{AB}$=$\frac{1}{2}$.