《2025年名师面对面满分特训方案九年级数学全一册人教版台州专版》

7. 九年级2班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形、等腰三角形(底边靠墙)、半圆形这三种方案,最佳方案是( )
A.方案1
B.方案2
C.方案3
D.方案1或方案2

答案： C

8. 如图,在Rt△ABC中,∠C= 90°,∠B= 30°,AB= 12 cm,点P是AB边上的一个动点,过点P作PE⊥BC,PF⊥AC,当PB= ______时,四边形PECF的面积最大,最大值为______.

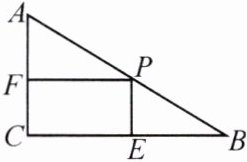
答案： 6 cm 9√3 cm²

9. 如图,用一根60 cm的铁丝制作一个“日”字型框架ABCD,铁丝恰好全部用完.
(1)若所围成的矩形框架ABCD的面积为144平方厘米,则AB的长为多少?
(2)矩形框架ABCD面积的最大值为______.

答案： 解:
(1)设框架的长 AD 为$x\mathrm{cm}$,则宽 AB 为$\frac {60-2x}{3}\mathrm{cm}$,$\therefore x\cdot \frac {60-2x}{3}=144$,解得$x=12$或$x=18$,$\therefore AB=12\mathrm{cm}$或$AB=8\mathrm{cm}$,$\therefore AB$的长为 12 cm 或 8 cm.
(2)150 cm²

10. 为落实国家《关于全面加强新时代大中小学劳动教育的意见》,某校准备在校园里利用围墙(墙长12 m)和21 m长的篱笆墙,围成Ⅰ、Ⅱ两块矩形劳动实践基地.某数学兴趣小组设计了两种方案(除围墙外,实线部分为篱笆墙,且不浪费篱笆墙),请根据设计方案回答下列问题:
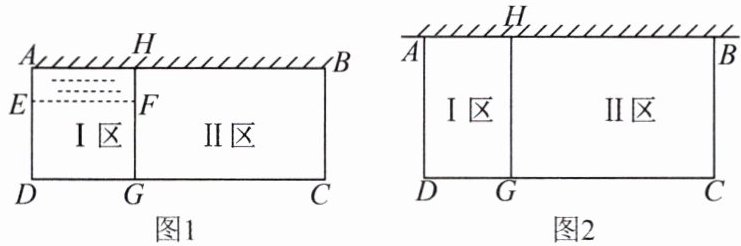
(1)方案一:如图1,全部利用围墙的长度,但要在Ⅰ区中留一个宽度AE= 1 m的水池,且需保证总种植面积为$32 m^2,$试分别确定CG,DG的长.
(2)方案二:如图2,使围成的两块矩形总种植面积最大,请问BC应设计为多长?此时最大面积为多少?

答案： 解:
(1)$\because (21-12)÷3=3(\mathrm{m})$,$\therefore$Ⅰ、Ⅱ两块矩形的面积为$12×3=36(\mathrm{m}^{2})$,设水池的长为$a\mathrm{m}$,则水池的面积为$a×1=a(\mathrm{m}^{2})$,$\therefore 36-a=32$,解得$a=4$,$\therefore DG=4\mathrm{m}$,$\therefore CG=CD-DG=12-4=8(\mathrm{m})$,即 CG 的长为 8 m,DG 的长为 4 m.
(2)设 BC 长为$x\mathrm{m}$,则 CD 长度为$(21-3x)\mathrm{m}$,$\therefore$总种植面积为$(21-3x)\cdot x=-3(x^{2}-7x)=-3(x-\frac {7}{2})^{2}+\frac {147}{4}$,$\because -3＜0$,$\therefore$当$x=\frac {7}{2}$时,总种植面积有最大值为$\frac {147}{4}\mathrm{m}^{2}$,即 BC 设计为$\frac {7}{2}\mathrm{m}$时总种植面积最大,此时最大面积为$\frac {147}{4}\mathrm{m}^{2}$.