第21页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
8.某广场中心有高低不同的各种喷泉,其中一支高度为3/2米的喷水管喷水最大高度为4米,此时喷水水平距离为1/2米,在如图所示的坐标系中,这支喷泉的函数关系式是 ( )
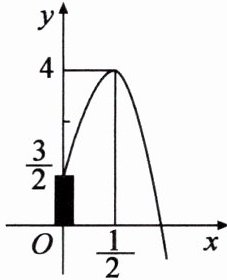
$A.y= 1/2x^2+4$
$B.y= -10(x+1/2)^2+4$
$C.y= 4(x-1/2)^2+2/3$
$D.y= -10(x-1/2)^2+4$

$A.y= 1/2x^2+4$
$B.y= -10(x+1/2)^2+4$
$C.y= 4(x-1/2)^2+2/3$
$D.y= -10(x-1/2)^2+4$
答案:
D
9.已知二次函数$y= ax^2+bx+c,$当x= 2时,y有最小值-1,且抛物线与x轴两交点间的距离为2,则此二次函数的解析式为______.
答案:
y=x²-4x+3
10.如图所示,抛物线$y= ax^2+bx+4$经过点A(-3,0),点B在抛物线上,CB//x轴,且AB平分∠CAO,则此抛物线的解析式是______.
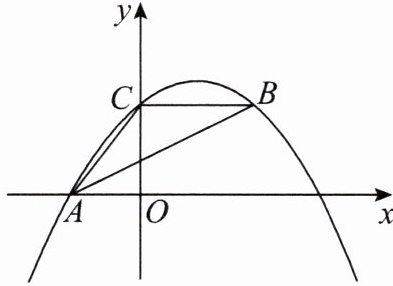

答案:
y=-1/6x²+5/6x+4
11.已知抛物线$y= mx^2+2mx+m^2-2.$
(1)求此抛物线的对称轴.
(2)若此抛物线的顶点在直线y= 2x+6上,求抛物线的解析式.
(1)求此抛物线的对称轴.
(2)若此抛物线的顶点在直线y= 2x+6上,求抛物线的解析式.
答案:
解:
(1)x=-b/2a=-2m/2m=-1,
∴抛物线的对称轴为直线 x=-1.
(2)
∵抛物线的顶点在直线 y=2x+6 上,
∴把 x=-1 代入得 y=2×(-1)+6=4,将(-1,4)代入抛物线得 4=m-2m+m²-2,解得 m=3 或 m=-2,
∴抛物线的解析式为 y=3x²+6x+7 或 y=-2x²-4x+2.
(1)x=-b/2a=-2m/2m=-1,
∴抛物线的对称轴为直线 x=-1.
(2)
∵抛物线的顶点在直线 y=2x+6 上,
∴把 x=-1 代入得 y=2×(-1)+6=4,将(-1,4)代入抛物线得 4=m-2m+m²-2,解得 m=3 或 m=-2,
∴抛物线的解析式为 y=3x²+6x+7 或 y=-2x²-4x+2.
12.如图,四边形ABCD是菱形,点D的坐标是(0,√3),以点C为顶点的抛物线$y= ax^2+bx+c$恰好经过x轴上A,B两点.
(1)求A,B,C三点的坐标.
(2)求过A,B,C三点的抛物线的解析式.
(3)若将上述抛物线沿其对称轴向上平移后恰好过点D,求平移后抛物线的解析式,并指出平移了多少个单位.
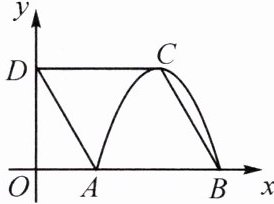
(1)求A,B,C三点的坐标.
(2)求过A,B,C三点的抛物线的解析式.
(3)若将上述抛物线沿其对称轴向上平移后恰好过点D,求平移后抛物线的解析式,并指出平移了多少个单位.

答案:
解:
(1)过点 C 作 CE⊥AB 于点 E,易知 Rt△AOD≌Rt△BEC,
∴OA=BE=AE,通过 Rt△AOD 的三边关系易求得 OA=1,DC=2,OB=3,
∴A,B,C 三点的坐标分别为(1,0),(3,0),(2,√3).
(2)设抛物线的解析式为 y=a(x-2)²+√3,代入点 A 坐标可得 a=-√3,
∴y=-√3(x-2)²+√3.
(3)设平移后抛物线的解析式为 y=-√3(x-2)²+k,代入 D(0,√3)可得 k=5√3,所以平移后抛物线的解析式为 y=-√3(x-2)²+5√3,它向上平移了 4√3 个单位.
(1)过点 C 作 CE⊥AB 于点 E,易知 Rt△AOD≌Rt△BEC,
∴OA=BE=AE,通过 Rt△AOD 的三边关系易求得 OA=1,DC=2,OB=3,
∴A,B,C 三点的坐标分别为(1,0),(3,0),(2,√3).
(2)设抛物线的解析式为 y=a(x-2)²+√3,代入点 A 坐标可得 a=-√3,
∴y=-√3(x-2)²+√3.
(3)设平移后抛物线的解析式为 y=-√3(x-2)²+k,代入 D(0,√3)可得 k=5√3,所以平移后抛物线的解析式为 y=-√3(x-2)²+5√3,它向上平移了 4√3 个单位.
查看更多完整答案,请扫码查看


