《2025年名师面对面满分特训方案九年级数学全一册人教版台州专版》

7.如图,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上.以C为中心,把△CDB旋转90°,则旋转后点D的对应点D'的坐标是( )

A.(2,10)
B.(-2,0)
C.(2,10)或(-2,0)
D.(10,2)或(-2,0)

答案： C

8.如图,在平面直角坐标系中,△OAB为等腰三角形,OA= AB= 5,点B到x轴的距离为4.若将△OAB绕点O逆时针旋转90°,得到△OA'B',则点B'的坐标为______.

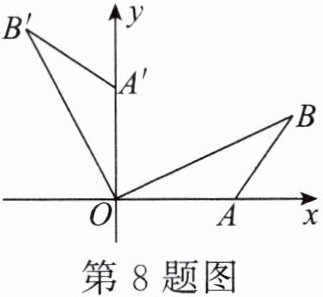
答案： (-4,8)

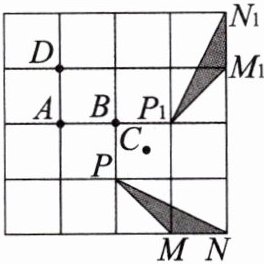
9.如图,在4×4的正方形网格中,小正方形的边长为1,△PMN绕某点旋转一定的角度,得到$△P_1M_1N_1.$
(1)指出旋转中心及旋转角的度数.
(2)求$MN_1$的长.

答案：
解:
(1)如图,连接BM,BN,BP,BM₁,BN₁,BP₁,则BP₁=BP=1,根据勾股定理得BM₁=BM=√5,BN₁=BN=2√2,
∴点B是旋转中心.由图中P和P₁点的位置关系可知,旋转角等于90°.
　　　　　　　　　　　　　　　　　
(2)根据勾股定理得MN₁=√(1²+4²)=√17,
∴MN₁的长是√17.

10.如图,在△ABC中,∠ACB= 90°,AB= 5,BC= 4,将△ABC绕点C顺时针旋转90°,若点A,B的对应点分别是点D,E,画出旋转后的三角形,并求点A与点D之间的距离.
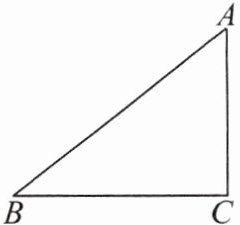
(不要求尺规作图)

答案：
解:如图,
　　　　　　　
∵在△ABC中,∠ACB=90°,AB=5,BC=4,
∴AC=√(AB²-BC²)=3.
∵将△ABC绕点C顺时针旋转90°,点A,B的对应点分别是点D,E,
∴AC=CD=3,∠ACD=90°,
∴AD=√(AC²+CD²)=3√2.

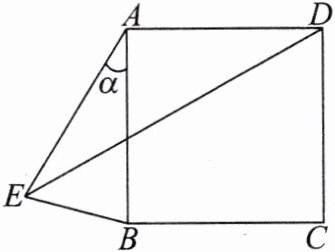
11.如图,四边形ABCD是正方形,以点A为中心,将线段AB顺时针旋转α(0°＜α＜90°),得到线段AE,连接DE,BE.
(1)求∠DEB的度数.
(2)过点B作BF⊥DE于点F,连接CF,依题意补全图形,用等式表示线段DE与CF的数量关系,并证明.

答案：
解:
(1)
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD.由旋转得∠EAB=α,AB=AE,
∴AE=AD,∠EAD=90°+α,
∴∠AED=45°-(1/2)α.
∵AE=AB,∠EAB=α,
∴∠AEB=90°-(1/2)α,
∴∠DEB=∠AEB-∠AED=45°.
(2)补全图形如下,线段DE与CF的数量关系为DE=√2 CF,
　　　　　　　
证明:过C作CG⊥CF交FD延长线于G.
∵BF⊥DE,
∴∠BFC+∠CFD=90°.
∵CG⊥CF,
∴∠CFD+∠G=90°,
∴∠BFC=∠G.
∵∠BCD=∠FCG=90°,
∴∠BCF=∠DCG,
∵BC=CD,
∴△BCF≌△DCG(AAS),
∴BF=DG,CF=CG,
∴△FCG是等腰直角三角形,
∴FG=√2 CF,由
(2)知,∠DEB=45°,
∴△BEF是等腰直角三角形,
∴EF=BF,
∴EF=DG,
∴EF+FD=DG+FD,即DE=FG,
∴DE=√2 CF.