第26页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1. 如图,某大门的形状是一抛物线形建筑,大门的地面宽8m,在两侧距地面3.5m高处有两个挂单位名牌匾用的铁环,两铁环的水平距离是6m.若按图所示建立平面直角坐标系,则抛物线的解析式是(建筑物厚度忽略不计)( )
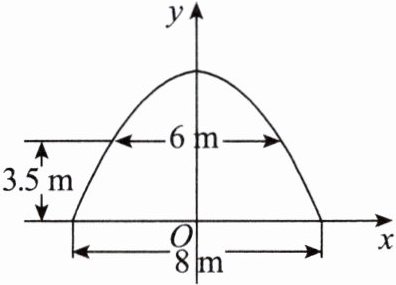
A.$y= -\frac{1}{2}x^{2}+8$
B.$y= -\frac{1}{2}x^{2}+7$
C.$y= \frac{1}{2}x^{2}+8$
D.$y= \frac{1}{2}x^{2}+7$

A.$y= -\frac{1}{2}x^{2}+8$
B.$y= -\frac{1}{2}x^{2}+7$
C.$y= \frac{1}{2}x^{2}+8$
D.$y= \frac{1}{2}x^{2}+7$
答案:
A
2. 如图,小明在某次投篮中,球的运动路线是抛物线$y= -0.2x^{2}+3.5$的一部分.若命中篮圈中心,则他与篮圈底的距离l是( )
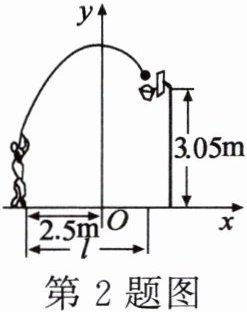
A.3m
B.3.5m
C.4m
D.4.5m

A.3m
B.3.5m
C.4m
D.4.5m
答案:
C
3. 如图,隧道的截面由抛物线和长方形OABC构成.按照图中所示的平面直角坐标系,抛物线可以用$y= -\frac{1}{6}x^{2}+2x+4$表示.在抛物线型拱壁上需要安装两排灯,如果灯离地面的高度为8m.那么两排灯的水平距离是( )
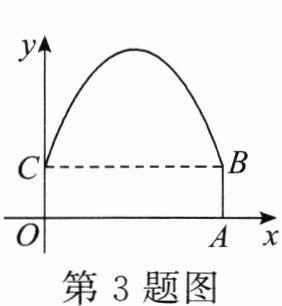
A.2m
B.4m
C.$4\sqrt{2}$m
D.$4\sqrt{3}$m

A.2m
B.4m
C.$4\sqrt{2}$m
D.$4\sqrt{3}$m
答案:
D
4. 某广场要建一个圆形喷水池,计划在池中心位置竖直安装一根顶部带有喷水头的水管,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心的水平距离也为3m,那么水管的设计高度应为______.
答案:
$\frac{9}{4}$ m
5. 小红看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:测得喷水头P距地面0.7m,水柱在距喷水头P水平距离5m处达到最高,最高点距地面3.2m;建立如图所示的平面直角坐标系,并设抛物线的表达式为$y= a(x-h)^{2}+k$,其中x(m)是水柱距喷水头的水平距离,y(m)是水柱距地面的高度.
(1)求抛物线的解析式.
(2)爸爸站在水柱正下方,且距喷水头P水平距离3m.身高1.6m的小红在水柱下方走动,当她的头顶恰好接触到水柱时,求她与爸爸的水平距离.
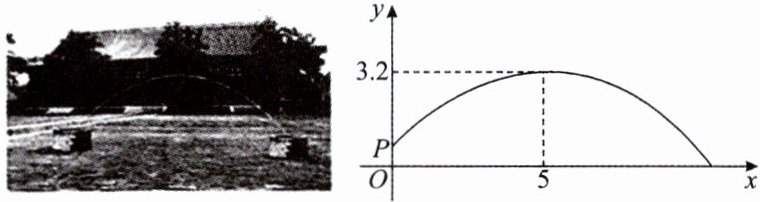
(1)求抛物线的解析式.
(2)爸爸站在水柱正下方,且距喷水头P水平距离3m.身高1.6m的小红在水柱下方走动,当她的头顶恰好接触到水柱时,求她与爸爸的水平距离.

答案:
(1)抛物线的解析式为$y=-\frac{1}{10}x^{2}+x+\frac{7}{10}$.
(2)当$y=1.6$时,$-\frac{1}{10}x^{2}+x+\frac{7}{10}=1.6$,解得$x=1$或$x=9$,
∴她与爸爸的水平距离为$3-1=2(m)$或$9-3=6(m)$,答:当她的头顶恰好接触到水柱时,与爸爸的水平距离是 2 m 或6 m.
(1)抛物线的解析式为$y=-\frac{1}{10}x^{2}+x+\frac{7}{10}$.
(2)当$y=1.6$时,$-\frac{1}{10}x^{2}+x+\frac{7}{10}=1.6$,解得$x=1$或$x=9$,
∴她与爸爸的水平距离为$3-1=2(m)$或$9-3=6(m)$,答:当她的头顶恰好接触到水柱时,与爸爸的水平距离是 2 m 或6 m.
查看更多完整答案,请扫码查看


