《2025年名师面对面满分特训方案九年级数学全一册人教版台州专版》

9.已知抛物线$y= (x-m)^{2}-(x-m)$,其中$m$是常数.
(1)求证：不论$m$为何值,该抛物线与$x$轴一定有两个公共点.
(2)若该抛物线的对称轴为直线$x= \frac{5}{2}$.
①求该抛物线的函数解析式；
②把该抛物线沿$y$轴向上平移多少个单位长度后,得到的抛物线与$x$轴只有一个公共点.

答案：
(1)证明:$y=(x-m)^{2}-(x-m)=x^{2}-(2m+1)x+m^{2}+m$,$\because \Delta =(2m+1)^{2}-4(m^{2}+m)=1＞0$,$\therefore$不论m为何值,该抛物线与x轴一定有两个公共点.
(2)解:①$\because x=-\frac {-(2m+1)}{2}=\frac {5}{2}$,$\therefore m=2$,$\therefore$抛物线解析式为$y=x^{2}-5x+6$;
②设抛物线沿y轴向上平移k个单位长度后,得到的抛物线与x轴只有一个公共点,则平移后抛物线解析式为$y=x^{2}-5x+6+k$,$\because$抛物线$y=x^{2}-5x+6+k$与x轴只有一个公共点,$\therefore \Delta =5^{2}-4(6+k)=0$,$\therefore k=\frac {1}{4}$,即把该抛物线沿y轴向上平移$\frac {1}{4}$个单位长度后,得到的抛物线与x轴只有一个公共点.

10.在羽毛球比赛中,某次羽毛球的运动路线可以看作是抛物线$y= -\frac{1}{4}x^{2}+\frac{3}{4}x+1$的一部分(如图所示,单位：m),则下列说法不正确的是 ( )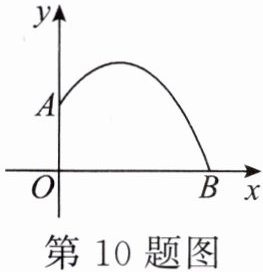

A.出球点$A离地面点O$的距离是1m
B.该羽毛球横向飞出的最远距离是3m
C.此次羽毛球最高达到$\frac{25}{16}m$
D.当羽毛球横向飞出$\frac{3}{2}m$时,可达到最高点

答案： B

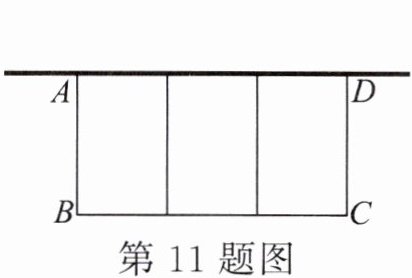
11.如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有两道篱笆的长方形花圃.设花圃的宽$AB为x$米,面积为$S$平方米,则$S与x$的函数关系式为______,花圃面积最大是______平方米.

答案： S=-4x²+24x 36

12.某商场销售一种进价为30元/个的商品,当销售价格$x$(元/个)满足$40＜x＜80$时,其销售量$y$(万个)与$x之间的关系式为y= -\frac{1}{10}x+9$.同时销售过程中的其它开支为50万元.
(1)求出商场销售这种商品的净利润$z$(万元)与销售价格$x$的函数表达式,销售价格$x$定为多少时净利润最大,最大净利润是多少？
(2)若净利润预期不低于17.5万元,试求出销售价格$x$的取值范围.若还需考虑销售量尽可能大,销售价格$x$应定为多少元？

答案： 解:
(1)$z=y(x-30)-50=(-\frac {1}{10}x+9)(x-30)-50=-\frac {1}{10}x^{2}+12x-320$,当$x=-\frac {b}{2a}=60$时,z最大,最大利润为$-\frac {1}{10}× 60^{2}+12× 60-320=40$.
(2)当$z=17.5$时,$17.5=-\frac {1}{10}x^{2}+12x-320$,解得$x_{1}=45$,$x_{2}=75$,$\because$净利润预期不低于17.5万元,且$a＜0$,$\therefore 45\leqslant x\leqslant 75$,$\because y=-\frac {1}{10}x+9$,y随x的增大而减小,$\therefore x=45$时,销售量最大.