《2025年名师面对面满分特训方案九年级数学全一册人教版台州专版》

9.小颖有两顶帽子,分别为红色和黑色,有三条围巾,分别为红色、黑色和白色,她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是 ( )

A.$\frac{1}{2}$
B.$\frac{2}{3}$
C.$\frac{1}{6}$
D.$\frac{5}{6}$

答案： C

10.在四张反面无差别的卡片上,其正面分别印有线段、等边三角形、平行四边形和正六边形.现将四张卡片的正面朝下放置,混合均匀后从中随机抽取两张,则抽到的卡片正面图形都是轴对称图形的概率为 ( )

A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{4}$
D.$\frac{3}{4}$

答案： A

11.从2名男生和2名女生中任选2名学生参加志愿者服务,那么选出的2名学生中至少有1名女生的概率是______.

答案： $\frac{5}{6}$

12.如图,将下列3张扑克牌洗匀后数字朝下放在桌面上.

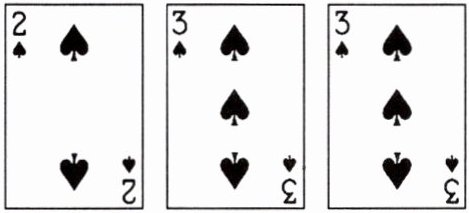
(1)从中随机抽取1张,抽得扑克牌上的数字为3的概率为______.
(2)从中随机抽取2张,用列表或画树状图的方法,求抽得2张扑克牌的数字不同的概率.

答案：

(1)$\frac{2}{3}$.　
(2)画树状图如下: 　共有6种等可能的结果，其中抽得2张扑克牌的数字不同的结果有4种，
∴抽得2张扑克牌的数字不同的概率为$\frac{4}{6}=\frac{2}{3}$.

13.如图,甲、乙两个转盘均被分成3个面积相等的扇形,每个扇形中都标有相应的数字,同时转动两个转盘(当指针指在边界线上时视为无效,需重新转动转盘),当转盘停止后,把甲、乙两个转盘中指针所指数字分别记为x,y.请用树状图或列表法求点$(x,y)$落在平面直角坐标系第一象限内的概率.

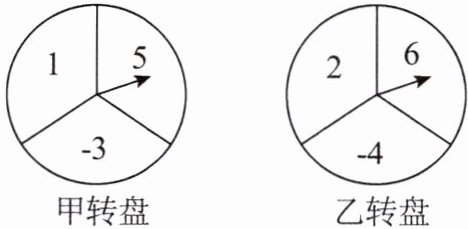
答案：
画树状图如图:　　　　　　 　共有9种等可能的结果，点(x,y)落在平面直角坐标系第一象限内的结果有4种，
∴点(x,y)落在平面直角坐标系第一象限内的概率为$\frac{4}{9}$.

14.甲、乙、丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,共传球三次.
(1)若开始时球在甲手中,求经过三次传球后,球传回甲手中的概率是多少.
(2)若乙想使球经过三次传递后,球落在自己手中的概率最大,乙会让球开始时在谁手中？请说明理由.

答案：

(1)画树状图如图:　　　　　　　　　　 　三次传球有8种等可能结果，其中传回甲手中的有2种.
∴P(传球三次回到甲手中)=$\frac{2}{8}=\frac{1}{4}$.　
(2)由
(1)可知:从甲开始传球，传球三次后球传到甲手中的概率为$\frac{1}{4}$，球传到乙、丙手中的概率均为$\frac{3}{8}$，
∴三次传球后球回到乙手中的概率最大值为$\frac{3}{8}$.
∴乙会让球开始时在甲手中或丙手中.